Introduction

From the perspective of the discounted cash flow model, the value of an ongoing business is a function of its operating results, cost of capital and the tax effect of financing and investment decisions. For the tax savings calculation, it is often assumed that the management of the Modigliani and Miller model (1963) or the Miller proposal (1977) are sufficient condition for its determination. The determination of the fiscal effects of debt has different aspects, depending on the tax systems in force in the markets where the company performs its activity. As a result, the company's value function applying the discounted cash flow model must be adapted to this management.

Nowadays, between the OECD Member countries and some South American countries (Argentina, Brazil, Paraguay and Uruguay), different types of tax systems are observed, being the degree of integration between corporate income and the dividend income obtained by the owner the common denominator. At one extreme the classical system with or without owners and creditors’ income tax is found . At the other extreme, systems where the corporate tax base is added to earnings as dividends, with different levels of integration are found.

The existence of taxes and tax systems introduces such a significant market imperfection that financing decisions and capital structure composition are relevant and affect the value of the company (Arzac and Glosten, 2005; Booth, 2007; De Angelo and Masulis, 1980; Dempsey, 2019; Fernandez, 2005; Graham, 1999; Massari et al., 2007; Miller, 1977; Miles and Ezzell, 1985; Modigliani and Miller, 1963; Molnár and Nyborg, 2011; Sick, 1990; Taggart, 1991; among others). Most of the literature deals with the tax effects derived from financing decisions on the company value assuming a classical income tax system, as it happens in the United States. There are few contributions that tackle the tax impact from the integrated tax systems perspective that is, with taxation imposed on bondholders and shareholders, as well as on the company. The contributions from Graham (2003, 2008), Niño et al. (2014) and Castillo et al. (2016) should be highlighted. Graham, studies the effects of classical and integrated systems and how they impact on the company´s value. On the other hand, Niño et al. classify seven taxation systems. Moreover, they propose a general model established in Castillo et al., applicable to all the systems.

The selected model should take into account the characteristics of the tax system since variables such as unlevered cost of capital, tax savings determination and weighted average cost of capital (WACC) will be modified in relation to its classic expression. For this reason, this paper focuses on the tax impact on value, in the light of the tax system, exposing the impact of the different systems on such variables. It should be noted that the financial cost rate to be used to quantify tax savings is not the subject matter of this paper, which is addressed in works such as those by De Angelo and Masulis (1980), Miles and Ezzell (1985), Sick (1990), Taggart (1991), Graham (1999), Arzac and Glosten (2005), Fernández (2005) and Booth (2007), among others. Next, this study describes and proposes the terms for the different tax systems in the OECD Member countries and Latin American countries, such as Argentina. First of all, we developed the different tax systems and the model adjusted to each of them, and then, through a case analysis, we studied the impact of the tax system on the variables such as company value, tax shield, weighted average cost of capital. This paper considers the generality of countries and tax system impacts, without considering specific particularities, for example the Argentine context and its tax system, such as inflation impacts on the variables of the company or on the taxation effect, considering that they deserve a detailed and specific management¹ . Finally, the main conclusions are developed.

Tax shields management in financial models.

In this section, we will explain the different models proposed to incorporate the analysis of the income tax effect on the variables of the company, such as funds flows, the company value, tax savings, cost of capital, as well as the tax effect of debt on the company value

Modigliani - Miller (1963): corporate tax, tax shield and taxation classical system.

The management of taxes on value arises from a correction that the authors make to their classic publication (Modigliani and Miller, 1958). They incorporate in their analysis the advantages for a levered company by the tax saving of the debt. They also admit that the indebtedness has a tax advantage, due to the deduction of the interest in the income tax. The tax rate and debt level remain fixed and it will be possible to deduct the total interest on the debt from the tax base for corporate tax. The model states that the value of a levered company is calculated by the following formula,

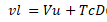[1]

$\mathit{\text{V}}l$: Value of the Levered Company

$\mathit{\text{V}}u$: Value of the Unlevered Company

$\text{T}c\times \text{D}$: Corporate tax rate by debt value

The value of the unlevered company arises from the ratio of the free funds flow (EBIT)² after operating income tax $\text{(}\text{FFL}(1-{\text{T}}_c))$ deducted from the rate of the cost of the unlevered capital³ (ku), ${\text{V}}_u=\frac{\mathit{\text{FFL}}(1-{\mathit{\text{T}}}_c)}{k_u}$ Tax savings (TS) arises from deducting the tax savings from the period (rTcD) from the rate of debt, (r), being$=\frac{\text{rTcD}}{\text{r}}$

As they adjust the expression corresponding to the cost of their equity It arises from the following equation

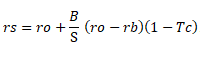[2]

1. rs: cost of equity

2. ro: cost of capital of the unlevered company

3. rb: cost of debt capital

4. $\underset{‾}{\mathit{\text{B}}}$

5. $\mathit{\text{S}}$: value of debt/ value of equity

6. Tc: Corporate tax rate

In this case, the tax savings as a debt ratio is represented by the corporate tax rate, without taking into account personal taxes. The value of equity (S) is the difference between the value of the levered company and the debt. $\text{S}={\text{V}}_l-\text{D}$

The cost of capital arises by leveraging and incorporating the tax shield into the unlevered cost.

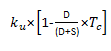[3]

Finally, the value of a levered company⁴ is expressed as follows

[4]

Miller (1977): Personal Taxes in a classical system

The model contemplates the existence of personal taxes on cash dividends and debt interests, where Tb represents the tax rate on debt interest for the creditor and Tsd the interest rate on cash dividends⁵ . After tax, cash flow is equal to $\text{FFL}=(1-{\text{T}}_c)\times (1-{\text{T}}_{sd})$. The cost-of-levered-capital rate arises from the following expression

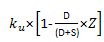[5]

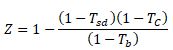[6]

When Tb=Tsd, then the tax shield is similar to the MM (TcD) model, where the company value remains similar to the classical model. If Tb>Tsd the tax shield will be lower than that in the MM model; same as the company value. If equity dividends have a differential rate, these models take them as cash dividends making specification mistakes. In the case that (1-Tb) = (1-Tc)(1-Tsd), tax savings is fully diluted.

General Model 2014: proposal for different tax systems

Niño et al. (2014) generalize the companies´ valuation model for a classical tax system and for a fully integrated one⁶. In this case, there should be considered the following variables: δ cash dividend distribution rate, k portion of tax base paid by the company attributable to the shareholder and b portion of corporate income tax that the shareholder can take as tax credit, from their tax determination. In addition, the tax reaches the dividend in cash and shares. For the latter the share is ${\mathit{\text{T}}}_{sg}$. The tax rate ${\mathit{\text{T}}}_s$ is the average between the cash dividends tax rate and share dividends tax rate, weighted by the distribution factor (δ), where: ${\text{T}}_{sg}=\delta \times {\text{T}}_{sd}+(1-\delta )\times {\text{T}}_{sg}$

[7]

The cost of the levered capital arises from the following expression.

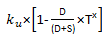[8]

Tax effect is explained as,

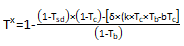[9]

The company value with debt, understanding its value as the cash flow it generates, is

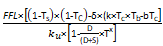[10]

The model is versatile and adapts to intermediate and integrated classical systems. It should be noted that in the case of non-integration and creditors’ income tax rate similar to dividend tax, all three models yield the same result. If this condition is not verified, the model that captures all the variables in the taxation systems is the general one.

Table 1 shows comparatively the models indicated for projected indicators (t+1).

Table 1

Free cash flows, cost of capital and company value adjusted with taxes under the three models

Tax systems

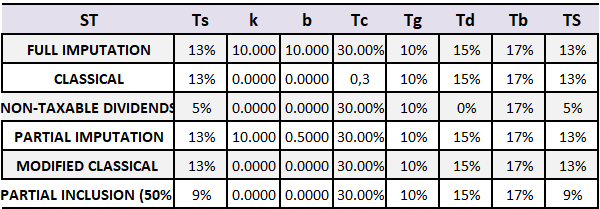
Tax systems are classified according to how corporate profits and shareholders' personal dividend income are taxed, taking into account any integration or tax relief to reduce double taxation. The seven tax systems among OECD Member countries are: 1. Classical system, 2. Modified classical system, 3. Partial inclusion system, 4. Non-dividend tax system, 5. Partial integration system, 6. Total integration system, 7. Other systems. Table 2 is set out below, classifying the corresponding tax structure and rates for OECD Member countries and Latin American countries. This section details the model applicable to each tax system: MG: General Model developed by Niño et al. (2014), MM: Model by Modigliani and Miller (1963) and M: Model developed by Miller (1977).

Table 2

Models and classification of tax systems country by country

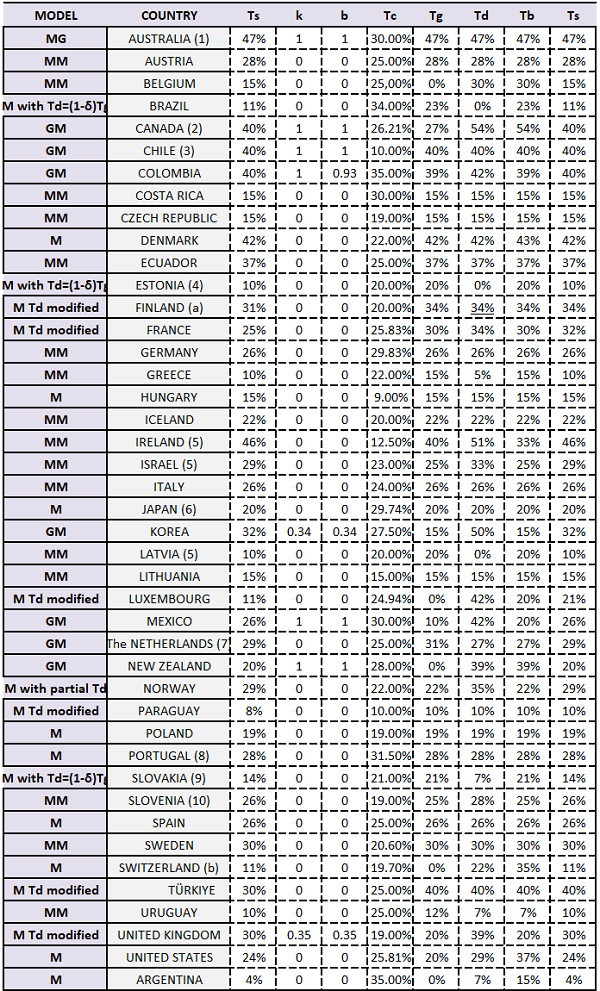
Note. Tc and Td are obtained from the Organization for Economic Co-operation and Development (s.f.-a) and Santander Trade (s.f.) for countries not included in the OECD Table II.4. In the case of Brazil, Ecuador, Paraguay and Uruguay, data for Tc, Td, Tg and Tb was obtained from PWC website (https://www.pwc.com/) and Deloitte (s.f.): (1) Australia: 50% of the proceeds from the sale of shares are taxed if they were held for at least 12 months (https://www.pwc.com/). Canada: 50 % of capital gains are taxed, the rate set out in Tg is 50 % of the nominal rate. Federal and provincial taxes are computed. (3) Chile: the company’s Tc rate in table II.1 of the OECD is 10%, representing a temporary reduction of the rate for 2020, 2021 and 2022. It corresponds to the Propyme system. It coexists in the country together with the fully integrated system (propyme), one partially integrated. (4) Estonia: the OECD table shows a 7% dividend rate. 7% applies to companies which tax at a reduced rate (Deloitte, s.f.). (5) Ireland, Israel and Latvia: they are classified as classical by the OECD but, because of Td is different from Tb reason why they are included in the group of modified classical. (6) Japan: previously framed as modified classical, currently classified by the OECD as "other" (OECD Table II.4 details that there are three methods for taxing dividends). (7) Netherlands: Table II.4 the OECD classifies it as classical in 2022, previously considered as partial imputation. (8) Portugal: Table II.4 the OECD classified it as modified classical, however, Td, Tg and Tb are the same, so it is considered classical. (9) Slovakia: previously classified without dividend tax, it currently taxes dividends at a 7% rate (10) Slovenia: classified as classical in the OECD and Td of 27.5% is indicated in PWC (https://www.pwc.com/); Deloitte (s.f.) considers Tsd Tsg and Tb of 25%.

Then, different expressions will be developed for the tax systems set out in the table above.

Classical System

In this system, corporate income tax and shareholders’ tax are separate and the dividends and interest income tax rate is the same(T_sd=T_b). In this system the tax shield is equal to the corporate tax rate, as shown in the following equation. In this case, the effects or distortions caused by the impact of inflation, usual as in Argentina´s context, are not considered.

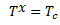[11]

For the calculation corresponding to the present value of tax savings as perpetual income taking a non-contingent approach, the classical expression is used

[12]

To calculate the weighted average cost of capital, expression (3) is used and the value of the levered company corresponds to equation (4).

Modified Classical System

This system presents, in relation to the classical system, the variant that dividends and interest on debt are taxed at different rates. There is no integration in this tax system between the tax paid by companies (Tc) and the tax paid by shareholders $\left({\mathit{\text{T}}}_{sd}\right)$. Therefore k=b=0. The periodic tax shield is derived from the following expression

[13]

Unlike Miller's proposal (1977), Ts represents in this case an average personal tax on dividends and capital gains as explained in the General Model equations. In this case, the dividend is distributed over the residual cash flow, this is $\text{FFR}=[\text{FFL}\times (1-{\text{T}}_c\left)\right]-r\times \text{D}$ where FFR represents the residual flow resulting from the difference between the free cash flow after corporate tax and the flow of interest and repayment of debt. In the event that the company is obliged by law to build up reserves from the income, it should consider these issues when applying the formula.

The value of tax savings in perpetuity is given by the formula below. The effect of the particularities of Argentina's income tax, which, for example, provides for the counting of accumulated losses from previous periods, is not considered in this case.

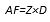[14]

The determination of the weighted average cost of capital, cash flows and value of the levered company follows the logic of Miller’s model (1977), where the rate T_sd is replaced by T_s

Partial dividend inclusion system

This system is characterized by the lack of integration between corporate taxes and shareholders’ taxes, as well as by taxing at the shareholder level only a portion of dividend income, in particular dividends in shares. The economic effect of this system is similar to taxing dividends at a lower rate⁷. The applicable expressions are the same as in the modified classical system, with a dividend effective rate ${\mathit{\text{T}}}_{sg}$ (*) arising from adjusting the nominal rate. To calculate the tax paid by shareholders the percentage of dividends subject to tax x% is applied on the ${\mathit{\text{T}}}_{sg}$ dividend tax rate. In this case, the formulas of the modified classical system are valid to calculate tax savings, cash flows, the weighted average cost of capital and the company value, with the exception that to calculate Ts the percentage of dividends that are taxed x% must be considered, as it arises from the following expression,

[15]

Cash Dividend Exemption system

In this system cash dividend income is not taxed $({\mathit{\text{T}}}_{sd}=0)$ capital gains income and corporate income are taxed. The expressions are similar to the classical system with the adjustment; $({\mathit{\text{T}}}_{sd}=0)$ and $\text{T}s=(1-\delta )\times {\text{T}}_{sg}$. The expressions to be used for calculating tax savings, cash flows, the weighted average cost of capital and the company value, are the same as those in the modified classical system, with the exception already stated for Ts.

Partial integration system

Under this system, a tax credit is granted to shareholders for part of the tax paid by the company (corporate tax). Shareholders consider dividend income to be dividends distributed in cash by the company plus a .- portion of corporate taxes. When calculating its taxable amount the shareholder computes the distributed dividend, δ×FFR×(1-Tc), plus a portion k of the corporate tax, calculated as: k×δ×Tc×FFL, as set out in Equation 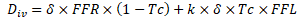16.

[16]

Some laws allow to deduct a smaller portion b, from the taxes paid by the company for their personal taxes ($k$=1,$b$<1). A portion b of the corporate tax calculated as: b×Tc×(FFL-r×D) is computed as the payment of the calculated dividend tax. In this case the tax paid by the shareholder $\mathit{\text{T}}{p}_s$ is,

[17]

The shareholder determines their tax base by adding the k portion of the imputed corporate tax to the dividends distributed applying the b portion of corporate tax that can be deducted as a tax credit. For the determination of the cost of capital, free cash flow after tax and the levered company value, the expressions corresponding to the General Model (2014) are applied. In this case, the tax savings per period comes from applying equation 9,

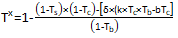[18]

The value of the tax shield in perpetuity arises from the product between savings and debt

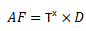[19]

The total tax paid by cash providers is derived from the following expression

[20]

Where the first part is the effect of the tax on dividends, the increase of the taxable base income by the integration factor and the tax credit. The second part adds the tax to the operating income and finally the third term represents the tax on debt interest.

Full imputation system

Also called total integration system, similar to the partial integration system, but the portion of increase corresponding to the taxable base is similar to the tax credit computable thus k=b=1. The same equations of the partial integration system are used: period tax savings (equation 9 and 18), current value of the stream of tax savings (equation 19), cost of capital (equation 8), value of the levered company (equation 10) and total tax determination (equation 20).

Other tax systems

There are specific systems that are beyond the logic of the integrated and classical systems, as in the case of Hungary where there is no integration. There is a differentiated management between listed or unlisted companies, imposing on the unlisted companies an additional percentage to be paid as contribution to the health sector. For the analysis, the case of listed companies is considered, so no changes are made to the tax rate considered. It is classified as a modified classical system, being these formulas applicable to calculate tax savings, cash flows, weighted average cost of capital and the company value.

Norway is another specific case, where the particularity that shareholders can deduct the risk-free market interest rate for their taxable dividends occurs, resulting Tsd a portion of the nominal tax rate. For the purposes of the analysis, the rate is not adjusted since the impact of the adjustment is not considered significant⁸. It is classified as a modified classical system, being these formulas applicable to calculate tax savings, cash flows, weighted average cost of capital and the company value.

Case study: the cash flow model and tax systems

In Table 3, the results of the different variables for the same company operating under the different tax systems analyzed, using the formulas of the general model, will be shown. In this way, it is demonstrated the impact of the tax system on these results.

Table 3

Variables of the company

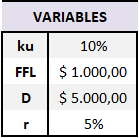
Assuming a total distribution of δ=0,50 dividends and similar tax rates for all tax systems as set out in the table below,

Table 4

Case study 1 Tax rate

We obtain the following results (Table 5)

Table 5

Case study 1 Profit/loss

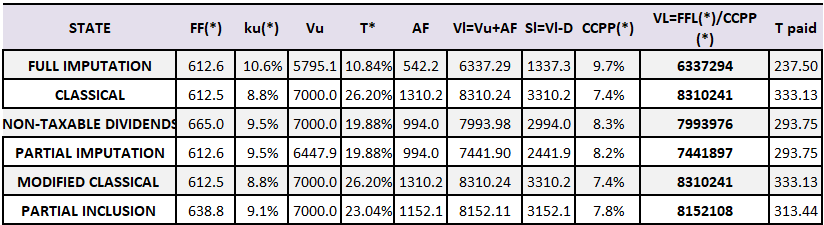
The highest value of cash flows occurs in the non-taxable dividend system because there are earnings available to be reinvested or distributed. Tax savings are higher in modified classical or classical systems because the tax effects of indebtedness are lower in a fully integrated tax system than those observed in a classical tax system (Niño et al., 2014, p. 127). The weighted average cost of capital is higher in a full imputation system because it has a higher required rate of return on capital and lower tax savings. Finally, it is observed that the total taxes paid are lower in the full imputation system due to the impact of integration that eliminates double taxation and therefore reduces tax savings.

Assuming now that we would like to obtain similar values from the levered company Vl for all tax systems, they should tax income according to the tax rate set out in Table 6 and we would obtain the profit/loss set out in Table 7.

Table 6

Case study 2 Tax rate

Table 7

Case study 2 Profit/loss

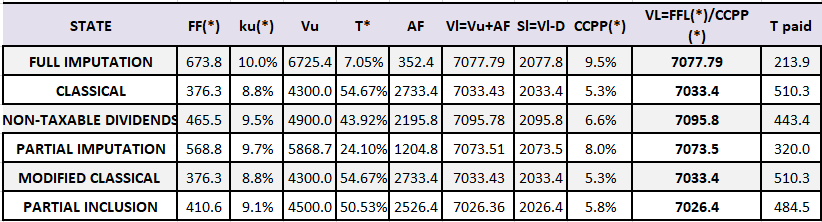
Higher rates of Tc are required in the modified classical and classical systems due to the lack of integration between corporate and personal taxes. Also, in this case, the greater effects of endebtedness in a classical system are observed (Niño et al., 2014, p. 127). The imputation system shows the highest weighted average cost of capital, due to the higher required return on capital and lower tax savings. The lower total tax value paid is therefore obtained in the full imputation system due to the low corporate tax rate and the effect of the integration between corporate and personal taxes.

If we now assume that we want to obtain the same weighted average cost of capital value modifying the debt tax rate and keeping the other variables constant, the different tax systems should tax profits according to the rates set out in Table 8 and we would obtain the profit/loss set out in Table 9

Table 8

Case study 3 Tax rate

Table 9

Case study 3 Profit/Loss

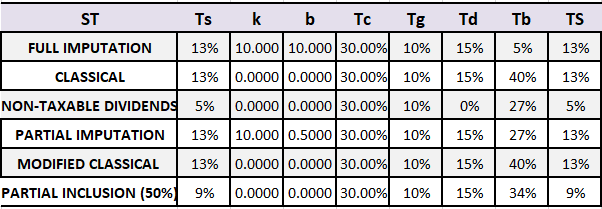
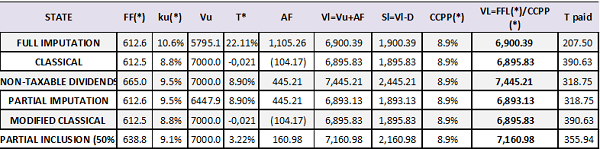
In this case, it is observed that, in the modified classical and classical systems, to balance the weighted average cost of capital, the debt interest tax rate must be increased in a proportion that cancels the tax benefit.

Conclusions

Tax effects involving cash outflows as savings should be jointly analyzed with the tax system where the company operates. The model proposed by Modigliani and Miller (1963) and Miller (1977) is often used, adapted in a way that the system that does not integrate corporate income with personal income and where dividends tax rate, regardless the type, is the same. In fact, these proposals are adapted to modified classical or classical systems. However, based on the OECD classification there are at least 7 income tax systems, ranging from the classical system to full integration systems. The general model is the one that best adapts to the different systems as it considers all the variables.

The tax system in which the company operates impacts on the variables, thus integrated systems require a higher cost of capital at similar rates and generate a lower tax shield and lower company value. On the contrary, at similar rates, a classical system generates higher tax shields, higher company Vl value and greater transfers of funds to the state as taxes.

Referencies

Arzac, E. y Glosten, L. (2005). A reconsideration of tax shield valuation. European Financial Management, 11(4), 453-461. https://doi.org/10.1111/j.1354-7798.2005.00292.x

Booth, L. (2007). Capital cash flows. APV, and valuation. European Financial Management, 13(1), 29-48. https://doi.org/10.1111/j.1468-036X.2006.00284.x

Castillo, A., Niño, J. y Zurita, S. (2016). Debt tax shields around the OECD world. Emerging Markets Finance and Trade, 53(1), 26-43. https://doi.org/10.1080/1540496X.2016.1145112

De Angelo, H. y Masulis, R. (1980). Optimal capital structure under corporate and personal taxation. Journal of Financial Economics, 8(1), 3-29. https://doi.org/10.1016/0304-405X(80)90019-7

Deloitte. (s.f). Tax guides and highlights. Recuperado en julio de 2022 de https://dits.deloitte.com/#TaxGuides

Dempsey, M. (2019). Discounting methods and personal taxes. European Financial Management, 25(2), 310-324. https://doi.org/10.1111/eufm.12157

Fernández, P. (2005). The value of tax shields is not equal to the present value of tax shields: a correction. WP SSRN, 1-8. https://ssrn.com/abstract=651206

Fernández, P. (2016). Valoración de empresas por descuento de flujos: 10 métodos y 7 teorías. SSRN. http://dx.doi.org/10.2139/ssrn.1266623

Graham, J. (1999). Do personal taxes affect corporate financing decisions? Journal of Public Economics, 73(2), 147-185. https://doi.org/10.1016/S0047-2727(99)00006-7

Graham, J. (2003). Taxes and corporate finance: A review. The Review of Financial Studies, 16(4), 1075-1129. https://doi.org/10.1093/rfs/hhg033

Graham, J. (2008). Taxes and corporate finance. En B. E. Eckbo (Ed.), Handbook of Corporate Finance –Empirical Corporate Finance (Vol. 2, Cap. 11). North Holland.

Massari, M., Roncaglio, F. y Zanetti, L. (2007). On the equivalence between the APV and the wacc approach in a growing leveraged firm. European Financial Management, 14(1), 152-162. https://doi.org/10.1111/j.1468-036X.2007.00392.x

Miles, J. y Ezzell, J. (1985). Reformulation tax shield valuation: a note. The Journal of Finance, 40(5), 1485-1492. https://doi.org/10.1111/j.1540-6261.1985.tb02396.x

Miller, M. H. (1977). Debt and Taxes. The Journal of Finance, 32(2), 261-275. https://doi.org/10.1111/j.1540-6261.1977.tb03267.x

Modigliani, F. y Miller, M. (Junio de 1958). The cost of capital, corporation finance and the theory of investment. American Economic Review, 48(3), 261-297. https://www.jstor.org/stable/1809766

Modigliani, F. y Miller, M. (Junio de 1963). Corporate income taxes and cost of capital: a correction. American Economic Review, 53(3), 433-443. https://www.jstor.org/stable/1809167

Molnár, P. y Nyborg, K. (2011). Tax-adjusted discount rates: a general formula under constant leverage ratios. European Financial Management, 19(3), 419-428. https://doi.org/10.1111/j.1468-036X.2011.00619.x

Niño, J., Zurita, S. y Castillo, A. (2014). Costo del capital e impuestos en un sistema tributario no integrado y en uno integrado: Generalización del modelo. El Trimestre Económico, 81(321), 109-132. https://doi.org/10.20430/ete.v81i321.110

Organización para la cooperación y el desarrollo Económicos (OCDE) (s.f.-a) Base de datos global estadísticas tributarias, tabla II.4. Recuperado en mayo de 2022 de https://www.oecd.org/tax/tax-policy/base-de-datos-global-de-estadisticas-tributarias.htm

Organización para la cooperación y el desarrollo Económicos (OCDE). (s.f.-b). OECD TAX DATABASE EXPLANATORY ANNEX Part II Taxation of corporate and capital income. Recuperado en mayo de 2022 de https://www.oecd.org/tax/tax-policy/tax-database/

Santander Trade (s.f). Establecerse en el extranjero. Fiscalidad. Recuperado en mayo de 2022 de https://santandertrade.com/es/portal/establecerse-extranjero

Sick, G. (1990). Tax-adjusted discount rates. Management Science, 36(12), 1432-1450. https://doi.org/10.1287/mnsc.36.12.1432

Taggart, R. (1991). Consistent valuation and cost of capital expressions with coporate and personal taxes. Financial Management, 20(3), 8-20. https://www.jstor.org/stable/3665747

Zurita, S., Castillo, A. y Niño, J. (2019). Inflation, tax integration and company valuation: The Latin American case. Journal of Business Research, 105, 370-380. https://doi.org/10.1016/j.jbusres.2018.03.041

Notes

Información adicional

Clasificación JEL: G30