Introducción

El presente artículo es la continuación de un grupo de investigaciones sobre las loterías de cupones realizados por el autor que buscan responder sobre la validez de las creencias que el apostador tiene sobre el juego. El primero estudió la creencia según la cual la zona de venta de los cupones podría influir en los sorteos y la segunda, la creencia sobre la influencia del peso de las bolillas en los resultados; esta tercera pretende construir un modelo de acción colectiva como estrategia ganadora por el apostador.

Las loterías de cupones han sido poco estudiadas de modo endógeno, en su mecanismo, aunque existen muchos trabajos vinculados con asuntos relacionados a su impacto; en los últimos 18 años, ha habido pocos estudios en Iberoamérica. Posiblemente la impronta dejada por los grandes economistas de los siglos XVIII y XIX haya impedido el interés en ella. A estos economistas siempre les sorprendió la falta de comportamiento estratégico en estos apostadores. Señala Garvía (2008) que William Petty catalogaba a los apostadores de tontos que se engañan a sí mismos por creer en la suerte o en la magia astrológica; Adam Smith lo atribuía a falta de cálculo de probabilidades y Marshall a errores por la emotividad del juego. Así mismo desde el marxismo se cree que estos son mecanismos tributarios y de dominación. Señala que desde la sociología se les ha prestado poca atención catalogando este comportamiento como irracional y hasta patológico; así, esta visión de algunos sociólogos resulta similar, por complementaria, a la de los economistas clásicos. Por el contrario, Garvía ofrece una mirada desde la “nueva” sociología económica que, para Muller (2016), acertaría al señalar que existen razones de imitación, lealtad al grupo e impulso en el comportamiento del apostador de las loterías; esto es, razones más sicosociales contra el racionalismo de los economistas clásicos o la carga ideológica de los marxistas. Añade Garvía que otras fórmulas explicativas han sido expuestas, relajando un tanto el concepto de racionalidad, como la de Savage (fundador de la teoría de juegos), que asume el riesgo en el juego como conducta racional (p. 3). El problema de estos planteamientos alternos es, para Garvía, que finalmente los modelos expuestos no pueden unificarse porque “zigzaguean las curvas de utilidad”, no se nos presentan suaves sino quebradas; no serían derivables, cosa incómoda a los matemáticos. Este asunto pertenece al clásico reduccionismo positivista que hoy tiene como alternativa la complejidad de los sistemas, por lo que actualmente habría que verlas bajo esta perspectiva.

Ciertamente el racionalismo no podría explicar las razones sociales ni económicas asociadas al juego (cosa que tampoco hace con muchos otros fenómenos económicos); Elster (1990) trata este asunto extensamente; de igual modo los marxistas clásicos, tratando al apostador como un enajenado, ofrecen una posición trivial. El racionalismo fracasa pues puede verse fácilmente que las preferencias no pueden ordenarse; esto es, preferir el producto a al b no implica que, si se prefiere b al c, entonces, tenga que preferirse a al c; en otras palabras, la tercera condición necesaria para construir una relación de equivalencia (la transitividad) y, por lo tanto, una métrica de preferencias, no es posible. De modo que hay que conformarse con comparaciones dos a dos o reflexivas. Puede verse, entre otros, a Resnik (1998).

Así, lo que a los economistas no les resulta obvio es que este apostador no tenga elección racional pues apuesta con una muy baja probabilidad de ganar resultando esto irracional; en la lotería que estudiamos la probabilidad de ganar con un cupón es 3,0x10^-7; esto es, comprar un cupón o combinación de 3.268.760 combinaciones no tendría sentido (estas resultan de combinar los primeros 25 números de 15 en 15); la conducta estratégica supone maximización de las expectativas y esto no sucede con las loterías. Sin embargo, estos sorteos se realizan semanalmente en muchos países; señala Garvía (2008) que en EEUU un 55% de ciudadanos, que viven en estados con loterías, las juegan, al menos, una vez al año. Igual sucede en España o en América Latina. Sin embargo, estos dos aspectos se conjugan en algo muy interesante, que se pasa por alto; decir que un tanto por cien juega “al menos una vez al año” no hace al apostador un fiel consumidor de loterías, sino un consumidor probable u ocasional en grado, salvando en parte la preocupación de los economistas. Esto es, el comportamiento del apostador no sería tanto más individual como estadístico, y multifactorial en lo sicosocial, haciendo muy compleja la aplicación de modelos determinísticos. A esto se une otro aspecto que, igualmente, suele pasarse por alto; en este juego el apostador no puede controlar ningún evento directamente vinculado con el sorteo; no puede incidir en las jugadas, como sí podría en otros juegos como el Dominó, el Blackjack, etc. Esto es, no puede incorporar su subjetividad. Pero sí podría hacerlo en eventos relacionados como incidir en la compra de cupones. De tal manera que ser un apostador ocasional o probable y poder incidir en las ventas hace que pueda configurarse una acción colectiva; por lo tanto, podemos preguntarnos ¿cómo es este comportamiento estadístico o grupal?, ¿habría conducta estratégica colectiva o una acción colectiva en el juego? Este estudio halla comportamientos de acción colectiva más allá del comportamiento individual y casual de compra de cupones.

El estudio se hizo sobre 40 sorteos semanales de una lotería en el año 2000 en Venezuela, durante los meses de enero a octubre a propósito de un proceso de auditoría, por lo tanto, la información es de fuente primaria; esto impone, sin embargo, una restricción, por limitaciones propias de espacio solo mostraremos los resultados directamente asociados con el objetivo de mostrar la acción colectiva y aquellos que sustenten su formación.

Formulación del problema

El proceso de mercadeo, previo al sorteo, supone la existencia de un mercado potencial (MP) de apostadores a los que se les ofrecen los cupones; se llaman boletas asignadas (a); en promedio se asignaron para ese año alrededor de 1,8MM cupones o boletas, cantidad muy por debajo del total de combinaciones posibles del juego (c). Las restantes, respecto de c, no están en el mercado, por lo tanto, no se asignan (na). De tal manera que el total de combinaciones se reparte entre a y na. Ahora bien, de las a, el mercado real u ocasional (MR) del sorteo absorbe una cantidad, son las boletas o cupones vendidos (v); en promedio se vendieron, para ese año, alrededor de 1,3MM. La diferencia respecto de v, son devueltas (d) al administrador del juego o Casa (C). Ahora bien, dado que el aleatorizador o bolillero es independiente del administrador (C) y de los apostadores (MR), todas las combinaciones juegan; esto es cada sorteo construye una combinación del total de combinaciones posibles, 3.268.760. La calidad de los procesos involucrados en cada sorteo es responsabilidad del administrador del juego y de las agencias gubernamentales encargadas de velar por la justeza de dichos procesos. La combinación sorteada puede resultar ganadora (g) o no ganadora (n); esto es, pudo ser vendida o quedar en Casa. Solo hay ganador (g) si fue vendida (v). Si la combinación resulta n, el premio se acumula en un bote hasta que resulte g. De esta manera todo el juego queda determinado por el azar, lo cual tiene una implicación importante, este crea rachas de g y n que no son predecibles, rachas aleatorias que dinamizan el juego creando expectativas sobre los resultados.

Nuestra hipótesis de trabajo, y la que queremos contrastar con la realidad mediante técnicas estadísticas corrientes, se fundamenta en la creencia de los apostadores según la cual, si se producen rachas n, se incrementa la participación de jugadores pues el bote aumenta. Es una hipótesis de nulidad pues es contrastable o falsable. Ahora bien, esta hipótesis supone que n debe tener un tamaño suficientemente grande que haga apetitosa la apuesta, pero no tanto que haga dudar de la aleatoriedad de la racha; por otra parte, supone que tal incremento de participantes no es casual dada la racha n. De esta manera si se producen tales rachas n se aceptaría una acción colectiva de MR sobre el bote; pero, por complemento, cuando no se produzcan estas rachas tendríamos una acción individual o aleatoria en el juego. Una limitación de este estudio es que al fundamentarse en pruebas empíricas solo se aportaría evidencia en favor de la estructura del juego acción individual-acción colectiva, pero, ontológicamente, la estaría evidenciando.

Metodología

Como hemos dicho, el total de combinaciones c se distribuye de la siguiente manera:

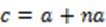(1)

Sin embargo, en el mercado, a se redistribuye así,

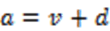
Sustituyendo en 1 queda

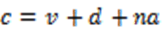
De esta estructura final de distribución de las combinaciones, v, las ventas, se corresponden con los apostadores o cooperadores; d, las devoluciones, se corresponden con los no cooperadores, pues son las boletas que el mercado devuelve por no absorberlas; finalmente, na, son las no asignadas y que no pueden colocarse pues sobredimensionarían el MP y que, de colocarse, serían devueltas. Además, tienen que participar en el juego pues el bolillero saca cualquiera de las combinaciones total.

Este hecho tiene implicaciones; primera, la incidencia en las ventas es un hecho probabilístico; las boletas vendidas contienen las posibilidades de que la suerte quede en MR; segundo, como v es un evento probable todas las demás variables lo son igualmente, esto es, d, y na; tercera, tendríamos que definir un jugador adicional y neutro que es el que retiene la apuesta (C), pero que es un jugador.

De esta forma, el método seguiría los siguientes pasos: en primer lugar, descartar la aleatoriedad de las rachas de las variables del proceso de mercadeo a través de una prueba respectiva; indicar que fue necesario construir una variable adicional, ganador, con ítems ganador(g) y no ganador (n), que sirva de recorrido o dominio de las demás (eje x); segundo, establecer el grado de control de MP sobre las ventas, a través de una correlación v vs d; tercero, establecer los momentos en donde MR ejerce su control sobre v, a través de una autocorrelación de las ventas; cuarto, construir las condiciones iniciales y finales del juego a través de las probabilidades a priori, fijadas por C, y las a posteriori dadas por la dinámica de MP a través de un perfil gráfico. En este ambiente observaremos la formación de las acciones individuales y colectivas y sus condiciones.

Desarrollo de las pruebas

Será necesario comprender que por motivos de espacio no nos extenderemos en la explicación de las pruebas, solo definiremos el arreglo de las variables en las pruebas; además, las pruebas son de las más usadas en estadística.

Pruebas de aleatoriedad a las variables

Las pruebas se hicieron sobre las variables ganador, boletas asignadas (a), boletas vendidas (v), boletas devueltas (d) y noasignadas (na). La tabla 1 muestra los resultados.

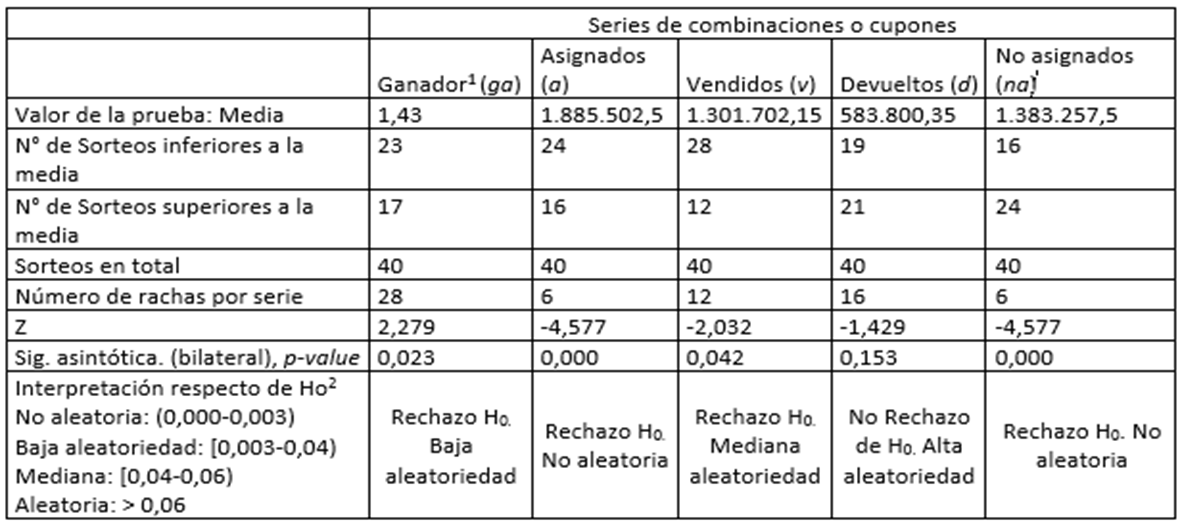
Tabla 1
Output de la prueba de SPSS19. Con una interpretación ad-hoc de la significación de H0 en la última fila.

1. Se ha definido una variable, ganador (g y n) para distinguir cuando la Casa acumula la apuesta (n)

2. H0= la serie es aleatoria

Fuente: libro de juegos de la lotería evaluada en 2000

El Valor de la prueba es la media; luego tenemos los resultados del número de sorteos que están por debajo y por encima de la media; seguidamente tenemos el número total de sorteos testeados; luego el número de rachas por cada serie; el valor Z_r obtenido y la prueba asintótica bilateral con α= 0,05; la hipótesis nula (H₀) es de aleatoriedad y es la que la prueba va a testear. Las rachas son calculadas comparando cada valor de la serie con la media; si es mayor se asigna un 1; si es menor, un -1; de modo tal que se cuentan los 1 y los -1 como rachas.

Los dos últimos renglones de la tabla 1 muestran los resultados. Con el objeto de ahorrar espacio, hemos creado una escala ad-hoc de interpretación del p-value de cada serie que puede verse en el último renglón. Hacemos un test de significación (TS) y no un test de hipótesis (TH), pues este se usa cuando tenemos una hipótesis alterna en toma de decisiones; nosotros no la tenemos por lo que asumimos el TS para ver el grado de aleatoriedad de las series. El punto focal en este test es que un entorno de 0,05 es difícil decidir o no la aleatoriedad (ver intervalo mediano de la escala). Puede verse una extensa discusión de esto en Prieto Valiente y Herranz Tejedor (2005).

Así, las series de combinaciones a y na no son aleatorias (0,000 << 0.05). Esto es consistente con las políticas del administrador del juego de distribuir según un plan de mercadeo. Ahora bien, ga ofrece la menor carga de aleatoriedad (0,023<0,05), pues es la que se aleja más del punto crítico hacia el rechazo de esta; lo que estaría indicando tendencia hacia n; el 57% de las series fueron de no ganadores^[1]. Por su parte, las series de vendidos (p-value = 0,042) aparecen con una mediana aleatoriedad (técnicamente se rechaza H₀) indicando que en las ventas tienen influencia de MR pues son los que cooperan en el juego; y devueltos (p-value = 0,153), donde no se podría rechazar H₀; esto es, sería la variable de más aleatoriedad; esto tendría sentido pues son los no cooperadores y que se incorporan al juego dependiendo de las circunstancias de este.

Adicionalmente, en favor de los economistas clásicos, las rachas de ventas, al tener una carga media de aleatoriedad, indican lo ocasional del juego. Por el contrario, la alta aleatoriedad de las devoluciones indica que pese a ser no cooperantes fluctúan entre esta posición y cooperar.

Correlación boletas vendidas vs. devueltas

Esta correlación tiene por objeto ver el grado de control que tendrían los cooperadores sobre las ventas de boletas. Una correlación negativa indica que a medida que los cooperadores compran boletas los no cooperadores disminuyen; esta relación puede verse en la ecuación 2, (v = a – d). El gráfico 1 muestra esta relación.

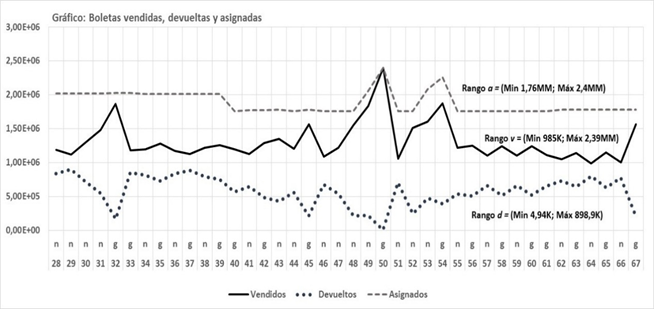
Gráfico 1
Evolución de las ventas y devoluciones en 40 sorteos en el año 2000. Se muestran los eventos donde hubo ganador o donde se acumuló.

El gráfico fue procesado con Excel.

Los valores de los sorteos deben leerse precedidos de 4. Así 428, 429, etc.

K: valores en miles

MM: Valores en millones

Fuente: libro de juegos de la lotería evaluada en 2000

Puede verse que la simetría de ambas curvas, v y d, es elevada; obsérvese que el administrador del juego o la Casa (C) mantiene constante las asignaciones (a) por tramos. Las devoluciones se corresponden con las que el mercado no absorbe. Igualmente, las curvas sugieren existencia de correlación entre ambas. La tabla 2 analiza este aspecto.

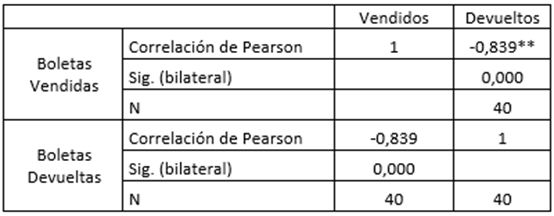
Tabla 2
Tabla de correlación de Pearson entre las series de vendidas y devueltas en 40 sorteos en el año 2000.

Correlación procesada con SPSS19

** La correlación es significante al nivel 0,01 (bilateral).

Fuente: libro de juegos de la lotería evaluada en 2000

Con un p-value de 0,000 puede descartarse la hipótesis de ausencia de correlación (H₀: ρ=0); esto indica que el mercado real o los cooperadores tienen un elevado control de las ventas, posiblemente, como contrapartida a no tener libertad en el juego.

Autocorrelación en las ventas

La autocorrelación de la serie vendidos, v, nos indica si el incremento de las ventas es o no casual; recordemos que esta serie tiene una aleatoriedad media en las rachas. Para realizar la prueba construimos dos series paralelas con las ventas; la dividimos en dos grupos, uno con un rezago y otro sin él, luego obtenemos la correlación de Pearson entre ambas. Veamos un ejemplo, supongamos que tenemos los valores {2, 4, 6, 23, 56, 8, 9} de una serie; para construir una serie paralela con un rezago tendríamos que tomar los valores a partir del segundo, así, {4, 6, 23, 56, 8, 9} de manera que podamos construir los pares (v_t-1, v_t); así tendríamos los pares {(2,4); (4,6); (6,23); (23,56); (56, 8); (8,9)}; es decir, la misma serie, pero corrida un tiempo, de manera que los pares que toma la ecuación sean el anterior y el siguiente. La tabla 3 muestra estos resultados.

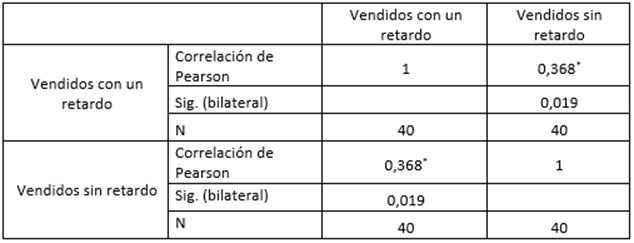
Tabla 3
Correlación entre las series vendidos con un retardo y vendidos en 40 sorteos de 2000.

Correlación procesada con SPSS19

*La correlación es significante al nivel 0,05 (bilateral).

Fuente: libro de juegos de la lotería evaluada en 2000

El coeficiente de correlación r(v_t-1, v_t), ofrece un valor bajo de 0,368 y un p-value de 0,019 que rechaza la hipótesis nula de ausencia de correlación por una de correlación media, resultando coherente con la prueba de rachas. Si tomamos en cuenta que la correlación positiva perfecta (r =1) se da en una línea monótona creciente, indicando que el valor t+1 siguiente, en ambas series, crece respecto del anterior t, podemos concluir que los puntos de autocorrelación son aquellos en los cuales v_t-1 < v_t. La gráfica 2 muestra esto con líneas punteadas.

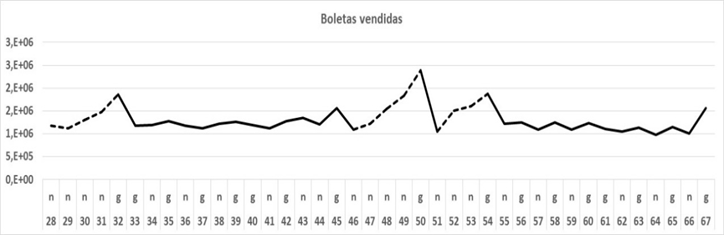
Gráfico 2
Evolución de las ventas en cuarenta sorteos en el año 2000. Se muestran los puntos de autocorrelación.

Los segmentos punteados indican autocorrelación.

Los valores de los sorteos deben leerse precedidos de 4. Así 428, 429, etc.

Gráfico realizado con Excel

Fuente: libro de juegos de la lotería evaluada en 2000

Hemos escogido tres segmentos de la curva donde se presenta autocorrelación parcial que coinciden con rachas de n; estos serían las rachas de los sorteos 28 a 31, la racha 46 a 50, y la racha 51 a 54; en todas ellas los sorteos son n seguidas por una racha g. En las rachas de no ganadores las ventas se incrementan mientras que en las demás las ventas caen o se mantienen por efecto del azar, pe., la racha de los sorteos 43 y 44 viene seguida de una racha ganador (la 45), pero en el sorteo 44 una porción de MR desiste decayendo las ventas. Puede verse que en el sorteo 32 hubo ganador luego de una racha de no ganadores; sin embargo, en el siguiente sorteo, 33, hubo ganador con ventas menores. Estaríamos observando dos comportamientos, uno aleatorio de g y n, y otro de autocorrelación de n acumulado que culmina con un g.

Probabilidades a priori y a posteriori

Ahora calcularemos y mostraremos las probabilidades asociadas al juego, para ver su dinámica y la relación entre los hallazgos anteriores. Estas son las probabilidades que salga una combinación asignadas (a) o no asignadas (na), devueltas (d) o vendidas (v).

Por la ecuación 1 podemos obtener las probabilidades teóricas.

Estas son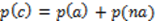

Esto es, las asignadas (a) son del mercado potencial, MP, y las no asignadas (na) son de la casa, C. Sin embargo, MP no va a absorber toda a por lo que devuelve una proporción d; esto hace que se incrementen las expectativas o que beneficie a C. De tal manera que las probabilidades se reparten así:

Como la probabilidad que salga una cualquiera es ,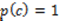

queda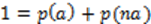

Por lo tanto, las probabilidades a priori son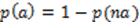

Ahora bien, previo al sorteo viene el proceso de mercadeo que consiste en el reparto de las boletas; así, de las asignadas (a) una proporción se vende (v) y otra se devuelve (d); de modo tal que las probabilidades a posteriori, con las que se juega, son el resultado de las ventas y las devoluciones. Las devoluciones (d) las acumula C, de modo que queda:

Dado que p(a) = p(v)+p(d)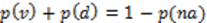

Probabilidades a posteriori serán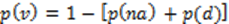

Perfil final de las distribuciones probabilísticas

Mostraremos estos resultados. Los gráficos 3 y 5 muestran los perfiles finales de las distribuciones de probabilidad de los 40 sorteos. El gráfico 3 muestra el perfil de las probabilidades a priori y el 5 las a posteriori. El gráfico 4 es de tránsito.

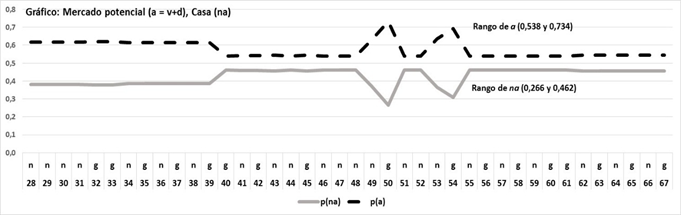
Gráfico 3
Probabilidades a priori del mercado potencial a= (v+d) y de la Casa (na).

Gráfico realizado con Excel

Los valores de los sorteos deben leerse precedidos de 4. Así 428, 429, etc.

Fuente: libro de juegos de la lotería evaluada en 2000

Puede verse en el gráfico 3 que las p(a) lucen constantes en el recorrido, solo alteradas por los sorteos 50 y 54 que hemos señalado como dos rachas de autocorrelación provocadas por MR. Lo significativo es que las probabilidades iniciales están a favor de los apostadores p(a), mientras que las de la Casa (C) p(na) son menores. La simetría de las curvas indica que son complementarias.

En el gráfico 4, se desglosan las probabilidades de las asignadas (a) en p(d) y p(v) con el objeto de apreciar el efecto de las devoluciones sobre p(na). La línea continua (p(na)) va a ser influenciada por la segmentada (p(d)) (ver gráfico 5) aleatorizándola, mientras que la línea punteada (p(v)) se mantiene igual.

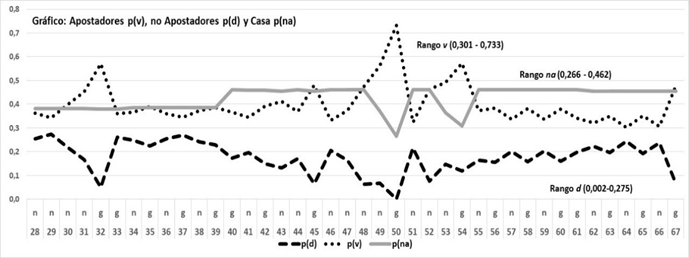
Gráfico 4
Desglose de las probabilidades de boletas asignadas (v,d) y no asignadas.

Gráfico realizado con Excel

Los valores de los sorteos deben leerse precedidos de 4. Así 428, 429, etc.

Fuente: libro de juegos de la lotería evaluada en 2000

En el gráfico 5, se muestran las probabilidades a posteriori o finales.

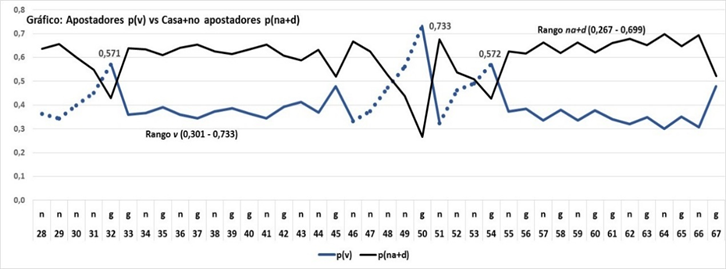
Gráfico 5
Probabilidades a posteriori. Boletas vendidas (v) y de la Casa (na+d). Las líneas punteadas de p(v) indican la acción colectiva o intencional, la línea continua la acción individual o aleatoria.

Gráfico realizado con Excel

Los valores de los sorteos deben leerse precedidos de 4. Así 428, 429, etc.

Fuente: libro de juegos de la lotería evaluada en 2000

Puede verse el efecto aleatorizante de p(d) sobre p(na) (curva superior, p(na+d)) y que revierte las probabilidades en favor de la Casa (C) pues p(v) queda por debajo. Sin embargo, se observa (líneas punteadas) cómo hay rachas n, p(v) > p(d + na) que afirman los dos comportamientos de los apostadores, uno aleatorio y otro con intencionalidad. Si revisamos el gráfico 1 veremos cómo C, a partir del sorteo 48, reacciona incrementando las asignaciones sobre una racha de n que venía produciéndose desde el sorteo 46 y que provocaba incrementos en las ventas. Lo mismo sucede en el tercer punto máximo observado en el sorteo 54; la racha de n venía produciéndose desde el sorteo 51 y es en el sorteo 52 cuando C reacciona incrementando las asignaciones. De modo que C reacciona luego que MR.

Discusión y conclusiones

De esta manera vemos en las pruebas que la aleatoriedad solo se rechaza, sin lugar a dudas, en las series de a y na; y que en las demás, v, d y ga, se ve comprometida por tendencias de v y d, así mismo, que existe correlación entre v y d como control de MR sobre las ventas y que estas ofrecen autocorrelación en los sorteos sobre todo en rachas n. Igualmente observamos que la influencia de p(d) sobre p(na) revierte las probabilidades, inicialmente en favor de MR hacia C; esto es, las d mostrarían a los no cooperadores. Igualmente observamos dos comportamientos en los apostadores, una acción colectiva y, por defecto, una individual; la primera intencional y la segunda, aleatoria.

Así, definiremos como acción colectiva a las rachas que cumplan las siguientes condiciones.

Rachas de dos valores (n y g), formadas por una serie n de al menos 3 elementos y una racha g final; por ejemplo, nnng, etc.

El valor de las ventas de la serie n debe ser menor o igual al anterior; esto es,

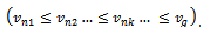
La probabilidad final de la racha de g, debe superar a la probabilidad de C; esto es,

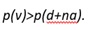
La primera condición garantiza la formación de la intencionalidad de MR, pues dos rachas como ng que reunieran las demás condiciones arrojaría dudas sobre si hubo intencionalidad o casualidad. La segunda condición muestra la intencionalidad; es posible que se den rendimientos decrecientes de v que acumulen el valor; pero esto arrojaría dudas sobre la intencionalidad de MR de acumular; finalmente, la tercera condición muestra el objetivo de la acción colectiva, revertir las probabilidades en favor de MR. Así, igualmente podría haber una racha que cumpla las dos primeras y no la tercera dando ganador a MR, pero sería un resultado aleatorio. Lo que le da suficiencia a la acción colectiva es la condición 3 de probabilidad. Las condiciones están destinadas a evidenciar la intencionalidad de MR más allá de rachas aleatorias.

Este proceso de acción colectiva implicaría un evento aleatorio de formación de rachas de n que, tras la acumulación del bote, despierte una oportunidad en MR para tomarlo incrementando las probabilidades en su favor; no podría presentarse un free rider o francotirador que esperaría por la acción de los demás para aprovecharse, como sucede en otros modelos de acción colectiva, pues tiene que ser un cooperador. La acción individual tiene otro sentido; dejaría que el azar decidiera la suerte de los apostadores, es más indiferente. Podemos concluir con algunas apreciaciones importantes y preguntas que, algunas, quedarán abiertas.

Primero, la acción individual o aleatoria y la colectiva tienen máximos locales de 47,9% y 73,3% de participación, respectivamente; la primera en un ambiente favorable a C, por lo tanto, no se darían rachas largas de g; la segunda favorable a MR. Segundo, la acción individual sería una participación con una elevada carga de indiferencia; la colectiva con intencionalidad; por lo tanto, el éxito de las jugadas individuales queda determinado por el azar, el de las colectivas, por acumulación de probabilidad. Tercero, en ambos mecanismos no existe posibilidad de desarrollo de destreza individual sobre el juego, como en otros como el Dominó o el Blackjack, por lo tanto, la acción individual es desinformada. Cuarto, podría dudarse de la acción colectiva aduciendo razones fortuitas; sin embargo, si la participación de MR fuese mayor disminuirían las rachas n; las rachas no las crea el bolillero sino el sesgo en las ventas. Quinto, estas acciones individual y colectiva estarían fundamentadas en el alto costo de oportunidad del bote^[2]. Sexto, resultaría difícil pensar que, si del bolillero salen combinaciones de modo aleatorio ¿cómo no se manifiesta esta aleatoriedad en las series y, por tanto, en las probabilidades? Una respuesta es que la combinación obtenida, sea cual sea, puede estar en manos de MR o de C; por lo tanto, el juego de probabilidades no se da sobre las del bolillero sino sobre las de las ventas. Séptimo, ¿por qué los no cooperadores permiten que las probabilidades queden en favor de C a través de d? ¿Es una consecuencia no intencional como señala Elster (1990)? Habría que tener en cuenta que la acción colectiva se nutre de no cooperadores; recordemos que este juego está formado por participantes ocasionales, no repetirían mucho, pero que es constante en las entradas y salidas de apostadores, de modo que ser cooperador o no es ad-hoc.

Referencias bibliográficas

Elster, J. (1990). Tuercas y Tornillos. Barcelona, España: Gedisa.

Garvía, R. (2008). Loterías. Un estudio desde la nueva sociología económica. Madrid: Centro de Investigaciones Sociológicas.

Instituto de Beneficencia Pública y Social del Estado Táchira. Lotería del Táchira. (2000). Libro de Juegos. San Cristóbal: Lotería del Táchira.

Muller, J. (23 de diciembre de 2016). El Juego que contradice la Teoría de Juegos. Recuperado de El Español: https://www.elespanol.com/economia/20161222/180361977_13.html

Prieto Valiente, L., & Herranz Tejedor, I. (2005). ¿Qué significa estadísticamente significativo? La falacia del criterio del 5% en la investigación científica. Madrid: Díaz Santos, S.A.

Resnik, M. D. (1998). Elecciones. Una introducción a la teoria de la decisión. Barcelona, España: Gedisa.

Notas

Información adicional

JEL: C72