1. Introducción

La idea de que los individuos de una economía pueden tomar decisiones que afecten su productividad futura nace prácticamente con Adam Smith en 1776. Sin embargo, fueron Becker (1962) y Schultz (1961) quienes definieron y formalizaron adecuadamente este concepto, estableciendo, al menos desde un punto de vista teórico, una clara conexión entre este y el crecimiento económico. Para Schultz, cualquier gasto realizado por una persona que implique mejorar su productividad futura debe ser considerado como inversión en capital humano. De esta forma, los principales conceptos que se vinculan con el capital humano de un individuo son la salud y la educación.

Schultz (1961) señala que el capital humano es necesario para poder operar el capital físico, con lo cual países con niveles bajos de capital humano verían limitado su crecimiento económico. Además, dado que los inversores privados solo invierten en capital físico, el capital humano resultaría ser el principal factor limitante del crecimiento económico.

Ahora bien, la definición propuesta por Schultz (1961) supone que el capital humano individual es un concepto complejo y, por lo tanto, su medición conlleva un conjunto de dificultades no menores. No obstante, muchos autores han tendido a identificar a la educación como el principal componente del capital humano. Esto se debe a que las personas, en edades tempranas, destinan gran parte de su tiempo a educarse, preparándose para su futuro. A su vez, es fácil establecer la conexión entre educación y productividad individual a través del efecto que el nivel educativo de una persona tiene sobre su salario.

Por estos motivos, diversos autores han estudiado la relación empírica existente entre años promedio de estudio de la población y PBI, o la relación entre matriculación a los distintos niveles académicos en un determinado año y tasa de crecimiento del PBI. Ahora bien, los resultados obtenidos por estos autores son dispares.

Por un lado, es evidente la correlación positiva que existe entre escolaridad a nivel agregado y PBI. Por otro, esta correlación no implica que sea la escolaridad la que impacte sobre el nivel de actividad de una economía. Muchos estudios muestran que el efecto de los años de estudio sobre el PBI es no significativo cuando se controla por otras variables adecuadamente.

Es posible que estas medidas agregadas de capital humano tiendan a sobre simplificar la verdadera relación que existe entre escolaridad a nivel individual y stock de capital humano agregado, y que esto, a su vez, comprometa la medición de la relación entre capital humano y PBI. Conocer adecuadamente la relación existente entre escolaridad y crecimiento económico es importante para evaluar los efectos de distintas políticas educativas que podrían llevarse a cabo con el fin de aumentar la escolaridad de la población o la calidad de dicha escolaridad.

En este trabajo se busca cómo estimar la relación entre los años de estudio de la población y el crecimiento económico mediante el impacto que los primeros tienen sobre el capital humano. Para ello, proponemos construir una medida agregada de capital humano basada en la relación entre el stock de capital humano de un individuo y su nivel de escolaridad, la cual podemos describir mediante el vínculo entre el ingreso personal y los años de estudio de un individuo. La metodología de agregación presentada en este trabajo tiene dos importantes beneficios en comparación con las metodologías comúnmente utilizadas. Por un lado, nos permite probar cómo funcionan especificaciones no lineales para la relación entre años de escolaridad individual y stock de capital humano agregado en las regresiones realizadas entre el PBI per cápita y el stock de capital humano. Particularmente, la especificación cuadrática entre años de estudio y capital humano individual construida en base a los resultados de la ecuación de Mincer ajusta mejor los datos y mantiene un coeficiente significativo en regresiones donde los años promedio de estudio y otras especificaciones, lineales y no lineales, dejan de ser significativos. Por otro lado, este tipo de agregación nos ayuda a entender cómo la distribución de la educación a lo largo de los distintos grupos etarios de un país impacta en el capital humano agregado. Esto permite realizar cálculos de corto plazo, como estudiar el impacto que podría tener el mantener un año más estudiando a la población que hoy en día está a punto de terminar sus estudios para incorporarse en el mercado laboral, es decir, la población que tiene entre 18 y 24 años.

El trabajo se encuentra estructurado de la siguiente forma: en la sección 2 revisamos los antecedentes del tema, en la sección 3 proponemos un modelo teórico con el cual derivamos cotas para el stock de capital humano agregado de una economía. En la sección 4 proponemos un algoritmo que nos permite disminuir la brecha entre las cotas superior e inferior del stock de capital humano. En la sección 5 construimos series relativas a las cotas de capital humano de cada país. En la sección 6 estimamos mediante el método de Mínimos Cuadrados Ordinarios Dinámicos (MCOD) la relación entre las cotas del capital humano y el nivel agregado de producción, lo que nos permite hacer cálculos de corto plazo respecto del impacto de la educación en el crecimiento económico. En la sección 7 repetimos el ejercicio econométrico agregando una medida de calidad educativa. Finalmente, en la sección 8 se presentan las conclusiones de este trabajo.

2. Antecedentes del tema

Sobre la base de los resultados a nivel microeconómico relativos a los efectos de la educación sobre el nivel de productividad de los trabajadores, los cuales fueron documentados por Psacharopoulos (1985), autores como Lucas (1988) y Romer (1990) introdujeron la idea de que el capital humano es uno de los principales factores que afectan al crecimiento económico. Y, bajo la concepción de que el capital humano podía ser representado principalmente a través de la educación agregada de la población, diversos autores propusieron formas de estimar el efecto que la escolaridad tiene sobre el nivel de producción agregada utilizando distintas medidas basadas en los años promedio de estudio de la población. Por ejemplo, Benhabib y Spiegel (1994) proponen los años promedio de educación de la población como variable proxy del stock de capital humano. Por su parte, Pritchett (2001) define el stock de capital humano como el valor actual de la prima salarial por educación. Según este autor, el capital humano de un país viene dado por $H=C{w}_0\left(e^{0.1s-1}\right)$, donde $C$ es el factor de descuento, $w_0$ es el salario de un trabajador sin educación, y $s$ son los años promedio de estudio de la población. Por otro lado, Lindhal y Krueger (2001) proponen medir el cambio porcentual en el stock de capital humano mediante la variación en los años promedio de educación.

Todos estos autores intentaron estimar el impacto de aumentar los años de educación sobre la tasa de crecimiento económico mediante regresiones lineales. En todos los casos, sin importar la forma de la función de capital humano utilizada, los resultados mostraron coeficientes no significativos para la escolaridad, y, en algunos casos, con signo contrario al esperado.

Por estos motivos, algunos autores comenzaron a cuestionar el hecho de considerar que un año de educación adicional tiene el mismo impacto, en todos los países, sobre la productividad de los individuos. Y, por esta razón, propusieron modelos donde relacionaban el crecimiento económico con los años de escolaridad de la población y con la calidad de dicha escolaridad, medida a través de distintos test internacionales. En general, estos modelos suponen una relación lineal entre capital humano, años de educación y calidad educativa.

Es así como Hanushek y Woessmann (2008) y Hanushek (2013), entre otros, evidencian que los años de escolaridad de la población no afectan al crecimiento económico, mientras que la calidad de dicha escolaridad sí lo hace. No obstante, Breton (2011) demuestra que tanto la calidad como la cantidad de escolaridad son determinantes significativos del crecimiento.

Por otro lado, Cohen y Soto (2007) consideran que la falta de significatividad en la relación entre crecimiento económico y años promedio de educación se debe, en gran medida, a errores de medición. Por este motivo, construyen una nueva base de datos, la que utilizan para estimar las mismas regresiones planteadas por Benhabib y Spiegel (1994), Pritchett (2001) y Lindhal y Krueger (2001). En todos los casos obtienen estimaciones de los parámetros con los signos esperados y, además, para las regresiones basadas en la especificación de los últimos autores los coeficientes resultan significativos.

Además, Bils y Klenow (2000) propusieron una medida más amplia del stock de capital humano basada en la ecuación de Mincer (1974). Concretamente, para estos autores el capital humano de un individuo, $h$, viene dado por $log\left(h\right)=c_{1}s+c_{2}x+c_3{x}^2$, donde $x=edad-6-s$ es una aproximación de la experiencia laboral, y para $c_1$, $c_2$, y $c_3$ utilizan los promedios de los coeficientes de la ecuación de Mincer obtenidos por Psacharopoulos (1985). De esta forma, el stock de capital humano de una economía viene dado por la suma de los stocks individuales. Calibrando el modelo teórico que proponen, estos autores encuentran que la escolaridad tiene un impacto sobre el crecimiento económico que es menor a un tercio de la correlación entre estas variables.

Todos los trabajos hasta aquí presentados utilizan algún tipo de medida lineal entre años de escolaridad y capital humano, con excepción del trabajo de Bils y Klenow (2000), quienes utilizan metodologías no basadas en regresiones lineales para obtener sus conclusiones.

En la siguiente sección presentamos un modelo teórico que, partiendo de la ecuación de Mincer, demuestra la posible existencia de una relación no lineal entre los años de estudio y el stock de capital humano individual. Luego, utilizaremos esta relación para construir series para el stock de capital humano agregado de cada economía.

3. Modelo Teórico

Tomemos la función de producción agregada aumentada por capital humano:

En esta ecuación $Y$ es la producción agregada de un país, $K$ es el stock de capital físico, $H$ es el stock de capital humano y $A$ es la productividad total de los factores.

A partir de esta función de producción, derivamos la función de capital humano de un individuo partiendo de la relación establecida por Mincer (1974), así como de sus posteriores formulaciones. Con este fin, supondremos que el stock de capital humano de un trabajador viene dado por:

$h_j:=f\left(s_j,x_j\right)$(2)

donde $s_j$ representa los años de estudio del individuo $j$ y $x_j$ su experiencia laboral. Respecto de la función de capital humano individual, $f$, suponemos que es continua, derivable y no decreciente en todos sus argumentos, y además está acotada en el intervalo $\left[1,h_{\max }\right]$. Este último supuesto se basa en la idea de que todos los individuos tienen un nivel mínimo de productividad, sin importar si han estudiado o si tienen algún tipo de experiencia laboral.

Por otro lado, también estamos suponiendo que la educación impacta hasta cierto punto en la productividad de una persona. Pasado este punto, aumentos en los niveles educativos pueden no hacer a la persona más productiva. A modo de ejemplo, un individuo que estudia una carrera universitaria y se desarrolla laboralmente, y luego estudia otra carrera completamente distinta, puede adquirir nuevos conocimientos, pero estos últimos estudios no necesariamente lo hacen más productivo en su carrera laboral inicial.

Consideramos, además, que el stock de capital humano agregado de una economía viene dado por la suma de los stocks individuales, es decir $H=\sum _{j=1}^n{h}_j$.

Bajo condiciones de competencia perfecta, a una unidad de capital humano se le paga exactamente su productividad marginal, que viene dada por $\frac{\partial Y}{\partial H}$. Por lo tanto, un trabajador $j$ con $h_j$ unidades de capital humano obtiene un ingreso equivalente a $w_j=\frac{\partial Y}{\partial H}{h}_j$.

Teniendo en cuenta la función de producción agregada que hemos propuesto, el logaritmo del ingreso del trabajador j se puede escribir como:

$\mathrm{l}\mathrm{o}\mathrm{g}{w}_j=\mathrm{l}\mathrm{o}\mathrm{g}\alpha +\mathrm{l}\mathrm{o}\mathrm{g}A+\left(1-\alpha \right)\mathrm{l}\mathrm{o}\mathrm{g}K-\left(1-\alpha \right)\mathrm{l}\mathrm{o}\mathrm{g}H+\mathrm{l}\mathrm{o}\mathrm{g}{h}_j$ (3)

Y, dado que el stock de capital humano agregado de la economía es la suma de los stocks individuales, podemos reescribir la ecuación anterior de la siguiente forma:

$\mathrm{l}\mathrm{o}\mathrm{g}{w}_j=\mathrm{l}\mathrm{o}\mathrm{g}\alpha +\mathrm{l}\mathrm{o}\mathrm{g}A+\left(1-\alpha \right)\mathrm{l}\mathrm{o}\mathrm{g}K-\left(1-\alpha \right)\mathrm{l}\mathrm{o}\mathrm{g}\sum _{j=1}^n{h}_j+\mathrm{l}\mathrm{o}\mathrm{g}{h}_j$ (4)

Esta última igualdad implica que el efecto marginal de la escolaridad sobre el salario para el individuo j viene dado por:

$\frac{\partial \mathrm{l}\mathrm{o}\mathrm{g}{w}_j}{\partial s_j}=-\left(1-\alpha \right)\frac{1}{\sum _{j=1}^n{h}_j}\frac{\partial h_j}{\partial s_j}+\frac{\partial \mathrm{l}\mathrm{o}\mathrm{g}{h}_j}{\partial s_j}$ (5)

Teniendo en consideración la ecuación de Mincer (1974), así como las formulaciones más nuevas de esta, el ingreso de un individuo se relaciona con su escolaridad y experiencia laboral de la siguiente forma:

$\mathrm{l}\mathrm{o}\mathrm{g}{w}_j=a_0+g\left(s_j\right)+a_1{x}_j+a_2{x}_j^2+{\epsilon }_j$ (6)

donde $a_1$ y $a_2$ son, respectivamente, los coeficientes de la experiencia y la experiencia al cuadrado en la ecuación de Mincer, y ${\epsilon }_{\mathrm{j}}$ incluye todas las restantes características que impactan en el salario del individuo. La ecuación de Mincer tradicional considera a math>g como una función lineal, pero autores como Belzil (2008) o Deschenes (2001) demuestran que $g$ podría ser una función convexa en $s$. Estas razones nos llevan a considerar que podemos representar a $g$ como una función polinómica de grado 1 o 2.

Luego, utilizando (5) y (6) podemos derivar la siguiente expresión:

$g^{\text{'}}\left(s_j\right)=-\left(1-\alpha \right)\frac{1}{\sum _{j=1}^n{h}_j}\frac{\partial h_j}{\partial s_j}+\frac{\partial \mathrm{l}\mathrm{o}\mathrm{g}{h}_j}{\partial s_j}$ (7)

Es así como de (7), y de los supuestos propuestos para h, deducimos que

$\frac{\partial \mathrm{l}\mathrm{o}\mathrm{g}{h}_j}{\partial s_j}\ge g^{\text{'}}\left(s_j\right)$ (8)

Por otro lado, podemos reescribir (7) de la siguiente forma:

$g^{\text{'}}\left(s_j\right)=-\left(1-\alpha \right)\frac{1}{H}\frac{\partial h_j}{\partial s_j}+\frac{1}{h_j}\frac{\partial h_j}{\partial s_j}=\frac{\partial h_j}{\partial s_j}\left(\frac{1}{h_j}-\frac{1-\alpha }{H}\right)$ (9)

Dado que $H\ge h_j$, se cumple que:

$\frac{1}{h_j}-\frac{1-\alpha }{H}\ge \frac{1}{h_j}-\frac{1-\alpha }{h_j}=\frac{\alpha }{h_j}$ (10)

De esta última relación se deduce:

$g^{\text{'}}\left(s_j\right)\ge \frac{\partial h_j}{\partial s_j}\frac{\alpha }{h_j}=\alpha \frac{\partial \mathrm{l}\mathrm{o}\mathrm{g}{h}_j}{\partial s_j}$ (11)

En resumen, de (8) y (11) tenemos que:

$g^{\text{'}}\left(s_j\right)\le \frac{\partial \mathrm{l}\mathrm{o}\mathrm{g}{h}_j}{\partial s_j}\le \frac{g^{\text{'}}\left(s_j\right)}{\alpha }$ (12)

Integrando (12) en el intervalo $\left[0,s_j\right]$ y teniendo en cuenta que la ecuación de Mincer implica que $g\left(0\right)=0$:

$g\left(s_j\right)\le \log h_j\left(s_j,x_j\right)-\log h_j\left(0,x_j\right)\le \frac{g\left(s_j\right)}{\alpha }$ (13)

Dado que hemos supuesto que el capital humano es no decreciente en $x_j$, si suponemos además que los coeficientes $a_1$ y $a_2$ son tales que el individuo se retira del mercado laboral antes de sobrepasar los $-\frac{a_1}{2a_2}$ años de experiencia, supuesto consistente con los resultados encontrados por Vera Rueda (2015) y Alejo y Funes (2021), podemos razonar en forma análoga para la experiencia y obtener:

$a_1{x}_j+a_2{x}_j^2\le \log h_j\left(s_j,x_j\right)-\log h_j\left(s_j,0\right)\le \frac{a_1{x}_j+a_2{x}_j^2}{\alpha }$ (14)

De (13) podemos escribir:

$g\left(s_j\right)+\mathrm{l}\mathrm{o}\mathrm{g}{h}_j\left(0,x_j\right)\le \mathrm{l}\mathrm{o}\mathrm{g}{h}_j\left(s_j,x_j\right)\le \frac{g\left(s_j\right)}{\alpha }+\mathrm{l}\mathrm{o}\mathrm{g}{h}_j\left(0,x_j\right)$ (15)

Evaluando (14) en $s_j=\; 0$:

$a_1{x}_j+a_2{x}_j^2\le \log h_j\left(0,x_j\right)-\log h_j\left(0,0\right)\le \frac{a_1{x}_j+a_2{x}_j^2}{\alpha }$ (16)

Y dado que hemos supuesto $h_j\left(0,0\right)=\; 1$:

$a_1{x}_j+a_2{x}_j^2\le \mathrm{l}\mathrm{o}\mathrm{g}{h}_j\left(0,x_j\right)\le \frac{a_1{x}_j+a_2{x}_j^2}{\alpha }$ (17)

Teniendo en cuenta esta última desigualdad y la desigualdad (15), podemos escribir:

$g\left(s_j\right)+a_1{x}_j+a_2{x}_j^2\le \mathrm{l}\mathrm{o}\mathrm{g}{h}_j\left(s_j,x_j\right)\le \frac{g\left(s_j\right)+a_1{x}_j+a_2{x}_j^2}{\alpha }$ (18)

De esta forma hemos obtenido una cota superior y una inferior para el stock de capital humano individual, la cual viene dada por:

$e^{m_j}\le h_j\le e^{\frac{m_j}{\alpha }}$ (19)

donde $m_j=g\left(s_j\right)+a_1{x}_j+a_2{x}_j^2$.

Y, consecuentemente, podemos obtener una cota superior y una cota inferior para el stock de capital humano agregado de una economía:

$\sum _{j=1}^n{e}^{m_j}\le H\le \sum _{j=1}^n{e}^{\frac{m_j}{\alpha }}$ (20)

4. Estimación de la cota superior para el stock de capital humano

Hasta aquí hemos logrado determinar que la función individual de capital humano está acotada entre dos funciones exponenciales. Dado que hemos supuesto que $h_j$ es continua y no decreciente en $s_j$, si agregamos el supuesto adicional de que $h_j$ puede ser aproximada por una función exponencial, de (7) podemos derivar la siguiente expresión:

$h_j=e^{\frac{m_j}{1-\left(1-\alpha \right){\psi }_j}}$(21)

donde ${\psi }_j$ representa la participación relativa del capital humano del individuo $j$ en el stock agregado de capital humano¹. Resaltamos que el supuesto aquí agregado es comúnmente utilizado en la literatura de contabilidad del desarrollo; como ejemplo de ello se pueden mencionar los trabajos de Bils y Klenow (2000) y World Bank (2020).

La expresión (21) demuestra que el aumento que obtiene un individuo en su productividad al aumentar sus años de educación es mayor al retorno que recibe por hacerlo, lo que entendemos como una externalidad positiva. Es posible entender esta externalidad como el efecto positivo que genera aumentar la productividad de un trabajador sobre la capacidad productiva de sus compañeros de trabajo debido a la interacción entre ellos.

Consideramos que $x_j={\mathit{edad}}_j-s_j-\; 6$, por lo que $m_j=g\left(s_j\right)+a_2\left({\mathit{edad}}_j-s_j-\; 6\right)+a_3{\left({\mathit{edad}}_j-s_j-\; 6\right)}^2$ y reescribimos (21) de la siguiente forma:

$h_j=e^{\frac{m_j}{{\beta }_j}}$(22)

con $\alpha \le {\beta }_j\le \; 1$.

Vimos que, al considerar ${\beta }_j=\; 1$, es probable que estemos subestimando el stock de capital humano del individuo. Buscaremos ahora un valor para ${\beta }_j$ que nos asegure sobreestimar el stock de capital humano y que disminuya el rango propuesto por la expresión (20).

De (21) y (22) deducimos que:

${\beta }_j=1-\left(1-\alpha \right){\psi }_j=1-\left(1-\alpha \right)\frac{h_j}{\sum _{j=1}^n{h}_j}$(23)

Es decir que cada ${\beta }_j$ depende del verdadero valor de $\alpha$, de la cantidad de individuos en la economía y del stock de capital humano del individuo $j$.

Si bien ${\beta }_j$ puede ser distinto para cada individuo, si tomamos el menor valor posible para este parámetro podemos asegurar que estamos sobreestimando el verdadero valor de $h_j$.

Para obtener una cota inferior para $\beta$ proponemos el siguiente algoritmo:

1. Fijamos un valor para $\alpha$ y para $n$
2. Tomamos un valor inicial arbitrario para beta $\left({\beta }_0\right)$, el cual puede ser 1.
3. Suponemos que $n-\; 1$ trabajadores tienen 0 años de estudio y 0 años de experiencia, lo que implica que $n-\; 1$ trabajadores tienen un capital humano igual a 1.
4. Suponemos que el n-ésimo trabajador de la economía tiene el máximo posible de años de estudio y de experiencia, 14.5 años de estudio² y 37 años de experiencia, y calculamos su stock de capital humano considerando el promedio de los coeficientes de Mincer propuestos por Montenegro y Patrinos (2014) como retorno promedio a la escolaridad, y por Bils y Klenow (2000) como retorno promedio a la experiencia. De esta forma, la combinación de los pasos 4. y 5. garantiza que el $\psi$ de este último trabajador sea máximo.
5. Teniendo en cuenta el valor propuesto ${\beta }_0$, calculamos ${\beta }_1$ de la siguiente forma:

   ${\beta }_1=1-\left(1-{\alpha }_{fijo}\right)\frac{e^{\frac{m\left(14.5;37\right)}{{\beta }_0}}}{\left(n_{fijo}-1\right)+e^{\frac{m\left(14.5;37\right)}{{\beta }_0}}}$(24)

   donde $m\left(14.5;65\right)=g\left(14.5\right)+0.052\times 37-0.0007\times {37}^2$.

6. Con ${\beta }_1$ volvemos a iniciar el proceso y lo repetimos hasta obtener un valor fijo para $\beta$.

Debemos resaltar que, considerando que g es una función continua en los años de estudio, para cada $\alpha$ y para cada n la expresión (24) representa una función continua definida en el intervalo $\left[\alpha ,1\right]$ sobre sí mismo, por lo que aplica el teorema del punto fijo de Brouwer.

Para $n\ge \; 1000$ el algoritmo da como resultado $\beta >\; 0.99$, sin importar el $\alpha$ dado ni la forma funcional de $g$ empleada, para la cual utilizamos polinomios de grado 1, 2 y 3, acorde a los trabajos de Belzil (2008) y Montenegro y Patrinos (2014). Es decir, que si interpretamos a $n$ como el número total de trabajadores de una economía deberíamos proponer un $\beta =\; 1$. Esto implica que la posible externalidad derivada en la ecuación (21) se pierde al considerar que cada trabajador se relaciona con todos los trabajadores restantes de la economía. No obstante, podríamos calibrar n de acuerdo a la cantidad de trabajadores con los que el individuo se relaciona realmente en su empresa. Esto quiere decir que podríamos considerar a n como la cantidad de empleados que tiene una empresa promedio. Poschke (2018) muestra que el 75% de las firmas para una muestra de 56 países tiene 10 trabajadores o menos. Si utilizamos este dato como imput para el algoritmo propuesto, este se vuelve muy sensible al valor de $\alpha$ utilizado y a la forma funcional empleada para g, y en todos los casos obtenemos un efecto de la educación sobre el stock de capital humano mayor al retorno privado calculado por la ecuación de Mincer³. A modo de ejemplo, con este valor de $n$ y una forma funcional lineal para $g$, con un $\alpha =\; 0.8$ obtenemos un $\beta =\; 0.89$, para $\alpha =\; 0.5$ tenemos un $\beta =\; 0.58$, y para un $\alpha =\; 0.3$ obtenemos un valor de $\beta$ levemente superior a $0.3$.

5. Construcción de las series de capital humano

Con los resultados obtenidos hasta el momento, basándonos es los datos sobre educación de Barro y Lee (2013) y proponiendo una forma funcional específica para g, es posible calcular cotas para el stock agregado de capital humano de cada país según:

$\begin{array}{r}\sum _{j=1}^l{L}_j{e}^{m_j}\le H\le \sum _{j=1}^l{L}_j{e}^{\frac{m_j}{\beta }}\end{array}$(25)

donde ahora $j$ representa a la j-ésima cohorte, $L_j$ representa la cantidad de trabajadores pertenecientes a dicha cohorte y $\beta$ es el valor final obtenido en base al algoritmo presentado en la sección anterior considerando $n=\; 10$.

De esta forma, podemos estimar el efecto que tiene la cantidad de educación de la población en el stock de capital humano al utilizar un método de agregación similar al de Bils y Klenow (2000). No obstante, en este trabajo proponemos utilizar los retornos actualizados por Montenegro y Patrinos (2014), quienes encuentran un retorno promedio mundial a la educación del 10% según una muestra de 139 economías.

Estos autores muestran que los retornos de los distintos países están muy concentrados alrededor de la media y tienen una distribución normal. Pero, además, encuentran que los retornos a la educación secundaria son inferiores a los de la educación primaria y terciaria. Esto nos lleva a considerar una tercera posibilidad para representar a la función g, una función polinómica de tercer grado.

Es así que, con las estimaciones de Montenegro y Patrinos (2014), utilizando los datos de educación de Barro y Lee (2013) y considerando las distintas formas funcionales mencionadas para $g$, lineal, cuadrática y cúbica, podemos construir series de capital humano basadas solamente en el nivel de educación de la población para 99 países con una periodicidad de 5 años entre 1960 y 2010.

Para la especificación lineal

$g\left(s_j\right)=a\times s_j,$

utilizamos un $a=\; 0.1$ acorde con el promedio de los retornos encontrados por Montenegro y Patrinos (2014). Para la especificación cuadrática

$g\left(s_j\right)=a\times s_j^2,$

calculamos a de forma tal que el retorno promedio a lo largo de los 14.5 años de estudio fuera del 10%, lo que implica $a=\; 0.0069$. Finalmente, para la especificación cúbica

$g\left(s_j\right)=a\times s_j^3+b\times s_j^2+c\times s_j,$

De acuerdo con los resultados presentes en la Tabla 1 del trabajo de Montenegro y Patrinos (2014), fijamos los valores $a$, $b$ y $c$ para que el retorno promedio a lo largo de los 14.5 años de estudio fuera del 10%, que el retorno promedio a lo largo de los 6 primeros años de estudio fuera del 10.6%, el retorno promedio de los segundos 6 años de estudio fuera del 7.2% y el retorno promedio de los últimos 2.5 años de estudio fuera del 15.2%. Para este último caso, la propuesta resulta en un sistema inconsistente de 4 ecuaciones lineales con 3 incógnitas, que resolvimos por mínimos cuadrados ordinarios.

Con el fin de explotar al máximo la información disponible, proponemos completar las series de capital humano basadas en años de educación y las series de años promedio de estudio con el método propuesto por Boot et al (1967). Si bien este método fue pensado originalmente para obtener las estimaciones mensuales de series con periodicidad anual o trimestral, puede ser generalizado para obtener una serie de mayor frecuencia a partir de otra serie de menor frecuencia. Cabe señalar que este método fue estudiado mediante simulaciones por Rodríguez Feijoo et al. (2001) y comparado con otros métodos comunes en la literatura de series de tiempo, como el propuesto por Denton (1971), que es una ampliación de la propuesta de Boot et al., pero que requiere datos adicionales para su implementación. Los autores muestran que, en general, el método aquí utilizado es el que aproxima mejor el comportamiento real de los datos.

Esta metodología consiste en estimar el crecimiento anual de la serie de capital humano (o de años promedio de educación) en base al verdadero crecimiento que hubo en cada periodo de 5 años. Es importante resaltar que el método tiende a suavizar la serie resultante. Este hecho se vuelve muy relevante cuando la serie presenta extremos locales en el periodo a estimar. No obstante, consideramos que tanto el stock capital humano como los años promedio de educación no deberían presentar estos problemas. Esto se debe a que ambas series están muy relacionadas con la población total. Por ejemplo, para que haya extremos relativos en el periodo a estimar de los años promedio de estudio es necesario que en un periodo de 5 años haya un crecimiento importante de la población con más años de estudio seguido de una fuerte disminución de dicha población o viceversa.

De esta forma, construimos series de capital humano y años de estudio anuales para el periodo 1960 y 2010 en base a las series quinquenales disponibles relativas al mismo periodo. En el apéndice detallamos como se aplica el método de Boot et al. (1967) para este caso particular.

6. Estimación econométrica

Para lograr el objetivo propuesto en este trabajo necesitamos obtener una estimación del coeficiente $\alpha$ de la ecuación (1) presentada en el modelo teórico. Para esto contamos con los datos sobre educación y retornos a la educación mencionados previamente, así como con los datos de producción, capital físico y población provenientes del trabajo de Feenestra et al. (2015).

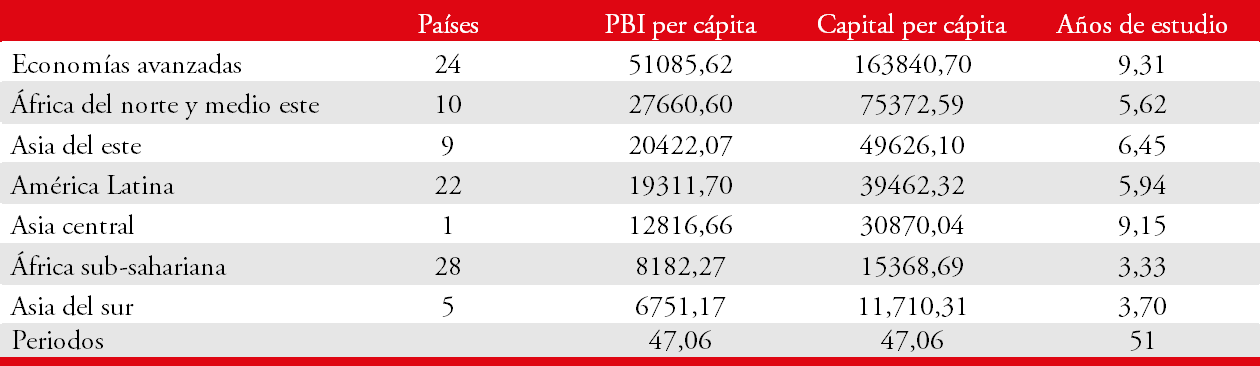
El Cuadro 1 muestra un resumen de los datos utilizados para el periodo 1960-2010, donde hemos agrupado las observaciones según las regiones propuestas por Barro y Lee (2013). Debemos resaltar que para construir la variable de PBI per cápita⁴, con el fin de medir únicamente la capacidad productiva de cada economía, utilizamos las variables rgdpo y emp de la base de Feenestra et al. (2015), las cuales contienen información sobre PBI real y cantidad de trabajadores de cada país respectivamente. Además, tomamos solo aquellos países para los cuales fue posible construir series sin datos faltantes desde el momento de inicio y con una cantidad mínima de 30 periodos.

El Cuadro 1 demuestra que las regiones con mayor cantidad de años de estudio y mayor capital por trabajador tienen un mayor nivel de PBI por trabajador. La última fila del cuadro muestra la cantidad de periodos promedio de cada serie de tiempo individual. Podemos ver que tenemos un panel de datos que no está completamente balanceado.

Cuadro 1

Resumen de las variables utilizadas

Fuente: elaboración propia en base a Barro y Lee (2013) y PWT 9.0.

Con los datos mencionados queremos estimar la siguiente relación:

$\log y_{it}=\log A+\left(1-\alpha \right)\log k_{it}+\alpha \log h_{it}+e_{it}$(26)

donde ahora $y_{it}$ representa el nivel de producción per cápita del país $i$ en el momento $t$, $k_{it}$ es el stock de capital físico per cápita y $y_{it}$ es su stock de capital humano per cápita. No obstante, dado que no conocemos la verdadera forma de la función de capital humano, la mejor opción es estimar:

$\log y_{it}=\log A+\left(1-\alpha \right)\log k_{it}+\alpha \log h_{it}^{\mathrm{*}}+{\epsilon }_{it},$(27)

donde $h^{*}$ es un factor del capital humano per cápita que depende solo de los años de escolaridad, el cual varía en función de la relación de Mincer considerada, y para el que podemos calcular una cota superior y una cota inferior según la metodología propuesta en la sección anterior. El término de error en esta última ecuación viene dado por:

${\epsilon }_{it}=\alpha C_{it}+{\tau }_{it},$

donde construimos $C_{it}=\log \left(h_{it}^{\mathrm{*}}\right)-\log \left(h_{it}\right)$. Es decir que estimar (27) implica obtener una estimación sesgada para $\alpha$, ya que $C_{it}$ termina siendo una variable omitida del modelo. No obstante, debemos tener en cuenta que $C_{it}$ es función de los años de estudio y de la experiencia de la población, y, por la forma en la que ha sido construida esta variable, considerando que $x_{jit}$ y $s_{jit}$ son los años de educación y de experiencia laboral del individuo $j$ en el país $i$ en el momento $t$ respectivamente, se cumple que $\frac{\partial C_{it}}{\partial s_{jit}}\ge \; 0$ y $\frac{\partial C_{it}}{\partial x_{jit}}\ge \; 0$ si consideramos la cota superior, y $\frac{\partial C_{it}}{\partial s_{jit}}\le \; 0$ y $\frac{\partial C_{it}}{\partial x_{jit}}\le \; 0$ si consideramos la cota inferior. Esto implica que:

$\mathrm{sign}\left(\mathrm{Cov}\left(\log h_{it}^{\mathrm{*}},C_{it}\right)\right)=\mathrm{sign}\left(\log h_{it}^{\mathrm{*}}-\log h_{it}\right)$(28)

Por lo tanto, si ${\widehat{\alpha }}^{\mathrm{*}}$ es el estimador obtenido de la regresión (27) y este estimador converge al aumentar el tamaño muestral, por el sesgo de variable omitida se cumple que:

$\mathrm{plim}{\widehat{\alpha }}^{\mathrm{*}}=\alpha +\frac{\left(\mathrm{Cov}\left(\log h_{it}^{\mathrm{*}},C_{it}\right)\right)}{\mathrm{Var}\left(\log h_{it}^{\mathrm{*}}\right)}$(29)

Por lo tanto, de (28) y (29) podemos deducir que:

$\mathrm{plim}{\widehat{\alpha }}_{max}^{\mathrm{*}}\le \alpha \le \mathrm{plim}{\widehat{\alpha }}_{min}^{\mathrm{*}},$

donde se utiliza la cota superior para obtener ${\widehat{\alpha }}_{max}^{\mathrm{*}}$ y la cota inferior para obtener ${\widehat{\alpha }}_{min}^{\mathrm{*}}$. En el apéndice demostramos mediante simulaciones de Montecarlo que el proceso de estimación propuesto en este trabajo asegura el cumplimiento de esta última relación. Los resultados de estas simulaciones se muestran en el Cuadro C del apéndice.

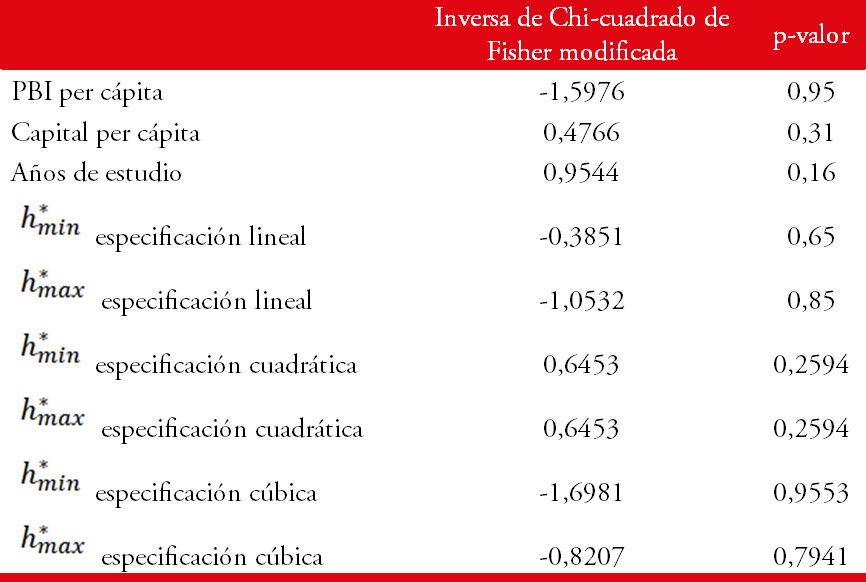
Dada la naturaleza de los datos con los que trabajamos, fue necesario testear la presencia de raíz unitaria en cada serie. Para esto llevamos a cabo el test propuesto por Choi (2001), el cual es un test tipo Fisher aplicable a paneles no balanceados. Para ninguna variable pudimos rechazar la hipótesis nula de que cada individuo presenta una serie integrada. Estos resultados se muestran en el Cuadro A del apéndice. Con este resultado procedimos a calcular los test de cointegración de Pedroni (1999). Los resultados de este test, presentados en el Cuadro B del apéndice, muestran cointegración por grupos o cointegración en panel según las distintas medidas de capital humano utilizadas.

Phillip y Moon (1999) demuestran que, para paneles grandes en cantidad de individuos y grandes en la dimensión temporal, la relación de largo plazo promedio entre las variables puede ser estimada consistentemente mediante el método de Mínimos Cuadrados Ordinarios (MCO), sin importar cuál sea la relación de cointegración entre los regresores y la variable explicada. Por otro lado, Kao y Chiang (2000) encuentran que en muestras finitas los estimadores de MCO pueden estar sesgados, mientras que el método de Mínimos Cuadrados Ordinarios Dinámicos (MCOD) produce estimadores insesgados tanto para paneles homogéneamente cointegrados como para paneles heterogéneamente cointegrados.

El Cuadro 2 muestra los resultados de las regresiones por MCO y MCOD(3,3)⁵ utilizando como posibles medidas de capital humano los años promedio de estudio y las cotas inferiores para las distintas especificaciones propuestas para el stock de capital humano per cápita, la cual llamamos $h_{\mathit{min}}^{*}$ y es calculada utilizando un $\beta =\; 1$. En la columna (1) se utilizó la especificación lineal para representar la ecuación de Mincer, mientras que en las columnas (2) y (3) se utilizaron las especificaciones cuadrática y cúbica respectivamente. Además, en todos los casos se utilizaron las regiones propuestas por Barro y Lee (2013) como variables de control y, con el fin de hacer inferencia estadística, los estimadores fueron corregidos por heterocedasticidad y autocorrelación utilizando el kernel de Bartlett según la propuesta de Jin et al. (2006).

Cuadro 2

Estimaciones MCO y MCOD utilizando las cotas inferiores

Fuente: elaboración propia en base a Barro y Lee (2013) y PWT 9.0.

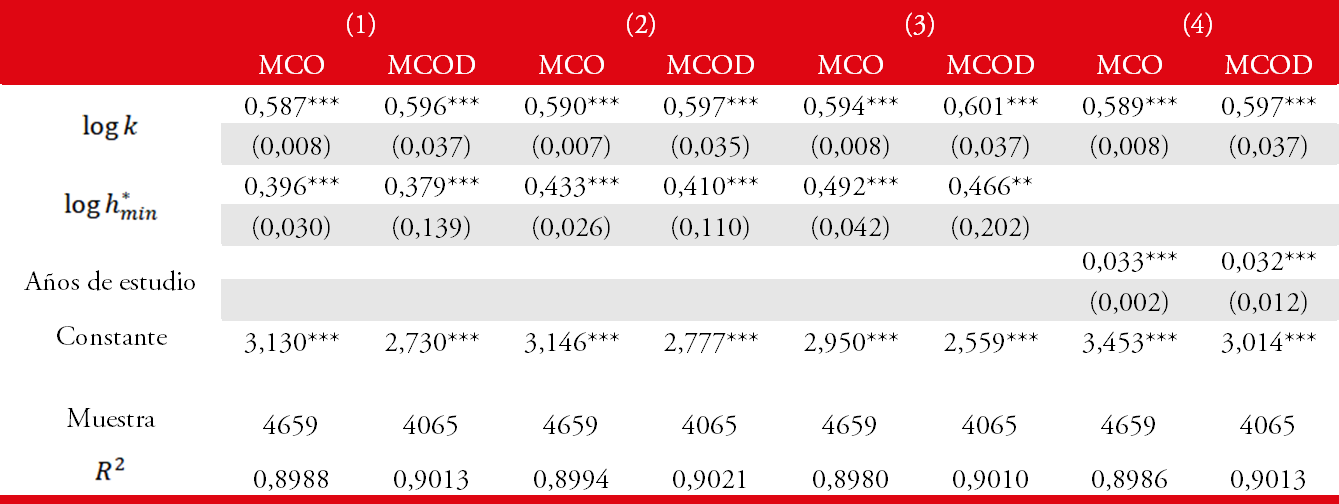
En primer lugar, debemos resaltar que los estimadores MCO son un poco mayores que los estimadores MCOD. Este resultado es similar al que encuentran Kao y Chiang (2000) mediante ejercicios de simulación. Por otro lado, en todos los casos el coeficiente del stock de capital físico per cápita no es significativamente distinto de 0.6. Esto implica que un $\alpha$ cercano a 0.4 es consistente con la teoría económica, lo que ocurre para la primera y segunda especificación. Cuando usamos la especificación cúbica obtenemos estimadores que suman un poco más de 1. Debemos tener en cuenta que el coeficiente estimado para los años promedio de educación debe ser dividido por 0.1 para ser comparado con el resto de las estimaciones. Por último, resaltamos que el mejor ajuste de los datos se produce cuando utilizamos la especificación cuadrática.

Cuadro 3

Estimaciones MCO y MCOD utilizando las cotas superiores

Fuente: elaboración propia en base a Barro y Lee (2013) y PWT 9.0.

Utilizamos los $\alpha$ estimados para calcular las cotas superiores del capital humano, h_max^*, mediante el algoritmo propuesto en la sección 3. De esta forma, con un $\alpha =\; 0.4$ como input obtuvimos un $\beta =\; 0.5$ para las especificaciones lineal y cúbica, y un $\beta =\; 0.85$ para el caso cuadrático. El Cuadro 3 muestra los resultados de las regresiones llevadas a cabo solo por MCOD utilizando las cotas superiores.

Los resultados de las regresiones presentadas en el Cuadro 3 muestran que, al disminuir $\beta$ en una proporción determinada, el valor de $\alpha$ estimado disminuye prácticamente en la misma proporción. Tanto para el caso lineal como en el cúbico, columnas (1) y (3), utilizamos un $\beta$ que es un 50% menor en comparación con el utilizado en las cotas inferiores, y obtuvimos reducciones en los parámetros estimados cercanas al 50%. Para la especificación cuadrática, columna (2), redujimos $\beta$ en un 15% y obtuvimos una reducción en el estimador del 14%. Además, la calidad de ajuste prácticamente no varía entre las estimaciones utilizando las cotas inferiores y superiores.

De acuerdo con estos resultados, podemos calcular que un aumento en los años promedio de educación de un año está asociado con un incremento en el PBI per cápita que varía entre un 3.2% y un 2.7% si consideramos la especificación lineal para la ecuación de Mincer, un 4.4% si tenemos en cuenta la especificación cuadrática, y un 3.6% si consideramos la especificación cúbica. Si consideramos los años promedio de estudio como medida del capital humano, un aumento en un 1 año de estos está vinculado con un crecimiento del PBI per cápita del 3.3%.

Los cálculos anteriores suponen que el aumento en los años de estudio se distribuye uniformemente a lo largo de toda la población. Esto quiere decir que somos capaces de agregar años de estudio tanto a la población que está a punto de insertarse en la fuerza laboral como a la que está por salir de ella por motivos de edad. En la realidad este hecho no ocurre, los años promedio aumentan a medida que se incorporan personas jóvenes con más años de estudio a la población económicamente activa. A modo de ejemplo, según los datos disponibles en la base de Barro y Lee (2013), para aumentar repentinamente en un año el promedio de estudio de una población es necesario mantener a los más jóvenes 5.73 años más en una institución educativa. Este incremento en los años de educación de la población más joven estaría asociado con un crecimiento que varía entre un 1.92% y un 1.39% si consideramos la especificación lineal, mientras que para las especificaciones cuadrática y cúbica sería cercano a un 4.9%.

Finalmente, calculamos que, si logramos aumentar, en el corto plazo, en un año la educación de la población más joven sería posible obtener un aumento en el PBI per cápita entre un 0.31% y 0.20% si consideramos la especificación lineal, entre un 0.47% y un 0.45% para la cuadrática, y entre un 0.28% y un 0.17% para la especificación cúbica. Al considerar los años promedio de estudio como medida de capital humano, estimamos un posible incremento del PBI per cápita del 0.57%, superior a todos los cálculos anteriores.

7. Controlando por calidad educativa

En esta sección vamos a introducir alguna medida de calidad educativa en nuestras estimaciones. Con este fin, proponemos una función de capital humano individual que sigue siendo consistente con el modelo teórico propuesto, la cual viene dada por:

$h_{qj}=q_j^{\phi }\times h_j,$

donde $h_{qj}$ es el stock de capital humano del individuo $j$, $q_j$ la calidad educativa recibida por dicho individuo, $\phi$ es un parámetro que toma un valor positivo, y $h_j$ es la función propuesta en el modelo teórico de este trabajo, la cual depende únicamente de los años de estudio y de la experiencia del agente⁶.

Altinok et al. (2018) presentan una base de datos sobre calidad educativa basada en test de educación internacionales y regionales. Homogeneizando las distintas medidas construyen un panel de datos para 163 economías que cubre el periodo 1965 a 2015. La base presenta datos faltantes; sin embargo, muestra que las distintas regiones tienden a agruparse por calidad educativa y no ha habido un gran cambio a lo largo del periodo estudiado⁷.

Dados los resultados consistentes con la teoría económica mostrados en el Cuadro 2, utilizamos la base propuesta por Altinok et al. (2018) para construir una medida más completa de capital humano utilizando las cotas para cada especificación de la ecuación de Mincer propuesta. Dado que no contamos con información desagregada relativa a calidad educativa, bajo el supuesto de que todos los individuos de un mismo país acceden a una educación de calidad igual o muy similar, consideramos que el stock de capital humano promedio de un país viene dado por:

$h_q=q^{\phi }\times h$(30)

donde ahora q hace referencia al resultado promedio en calidad educativa obtenido por el país según Altinok et al. (2018) en todo el periodo 1965-2015.

Esta especificación nos permite estimar la siguiente ecuación:

$\log y_{it}=\log A+\alpha \phi \log q_i+\alpha \log h_{it}^{\mathrm{*}}+\left(1-\alpha \right)\log k_{it}+{\epsilon }_{it}$(31)

El Cuadro 4 muestra los resultados de las nuevas regresiones estimadas por el método de MCOD al incluir como regresores las cotas inferiores. Una vez más la columna (1) corresponde a la especificación lineal para la ecuación de Mincer, mientras que las columnas (2) y (3) corresponden a las especificaciones cuadrática y cúbica respectivamente. Presentamos, además, los resultados obtenidos al utilizar como regresor la cota superior para el caso cuadrático en la columna (2').

Cuadro 4

Estimaciones considerando calidad educativa

Fuente: elaboración propia en base a Barro y Lee (2013) y PWT 9.0.

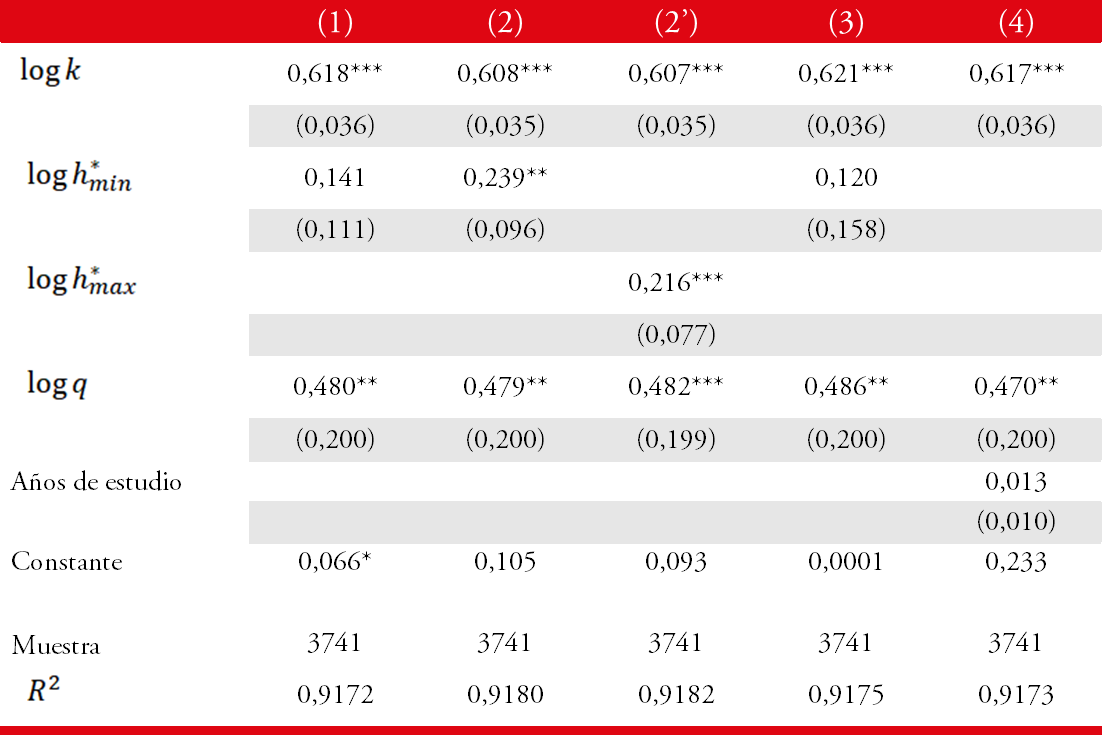
En primer lugar, debemos resaltar que, al agregar la calidad educativa, sin importar la especificación utilizada para la ecuación de Mincer, se produce una disminución considerable en el criterio de información de Akaike. En segundo lugar, notamos que al agregar una medida de calidad educativa, las medidas basadas en años de estudio dejan de ser significativas, salvo para los casos cuadráticos. Las especificaciones (2) y (2') muestran los mejores ajustes posibles, basados en el criterio de información de Akaike, y en ambos casos obtenemos una reducción importante en el parámetro estimado en relación a los resultados presentados en los Cuadros 2 y 3.

Esta reducción disminuye nuestras estimaciones de posible crecimiento en función del aumento en los años de educación de la población para la especificación cuadrática. Así, el aumento de un año en el promedio de años de estudio distribuido en forma uniforme a lo largo de la población estaría asociado con un crecimiento que varía entre un 2.64% y un 2.82% según consideremos la cota inferior o superior respectivamente. El aumento de 5.73 años de estudio en la población más joven estaría vinculado con un incremento del PBI per cápita que puede variar entre un 2.88% y un 3%. Finalmente, un aumento de un año en el promedio de estudio de la población más joven estaría relacionado con un crecimiento del 0.28% en el PBI per cápita para ambas cotas.

Por otro lado, la estimación de la ecuación (31) también nos permite calcular correlaciones entre variaciones del PBI per cápita y cambios en los años de estudio y/o en la calidad educativa. Con este fin, estimamos el posible incremento en el PBI per cápita para cada región estudiada si aumentara sus años de estudio y su calidad educativa de forma tal de llevar ambos al mismo nivel que el promedio de las economías avanzadas. El Cuadro 5 muestra los resultados obtenidos.

Cuadro 5

Crecimiento estimado para las distintas regiones

Nota: En base a los datos de Barro y Lee (2013) se consideraron dentro del grupo de economías avanzadas a Australia, Austria, Bélgica, Canadá, Dinamarca, Finlandia, Francia, Alemania, Grecia, Islandia, Irlanda, Italia, Japón, Luxemburgo, Holanda, Nueva Zelanda, Noruega, Portugal, España, Suecia, Suiza, Turquía, Reino Unido y Estados Unidos.
Fuente: elaboración propia en base a Barro y Lee (2013) y Altinok et al. (2013).

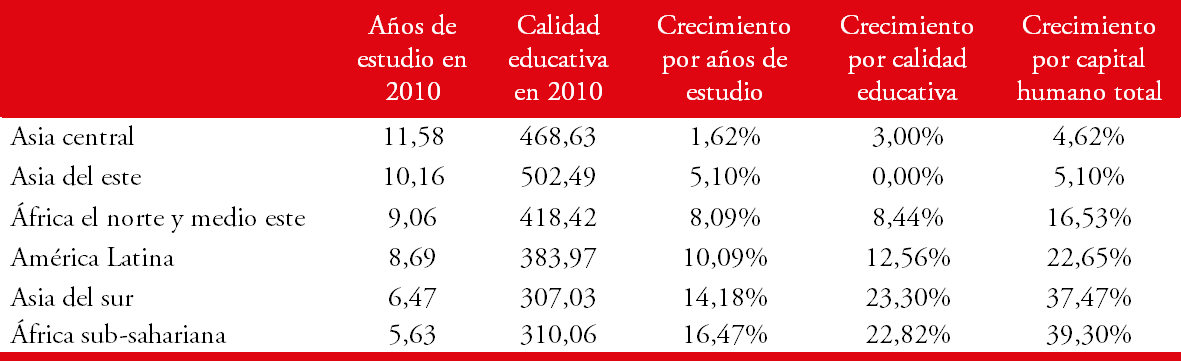
La mayoría de las regiones muestra estar en condiciones inferiores tanto en calidad como cantidad de educación con respecto a las economías avanzadas. Esto implica que existen beneficios potenciales por mejorar tanto la calidad de la educación ofrecida como por invertir en mantener más tiempo a la población estudiando. No obstante, es importante tener en cuenta que, de existir, estos beneficios pueden tardar el periodo de vida de una generación entera en manifestarse completamente. Dado que no contamos con datos desagregados de calidad educativa, no podemos estimar lo que puede suceder en el corto plazo al mejorar la calidad de la educación. A modo de ejemplo, podemos inferir que, si América Latina aumenta su calidad educativa a los niveles de las economías avanzadas hoy, tardaría 65 años en ver los efectos completos de esta medida, pero no sabemos cómo pueden manifestarse esos efectos en el corto plazo.

8. Conclusiones

Desde un punto de vista teórico, hemos logrado derivar cotas para el stock de capital humano individual en función de los años de estudio y experiencia laboral de cada agente económico. Además, propusimos un método que nos permitió reducir la brecha entre ambas cotas, específicamente disminuyendo la cota superior. De esta forma, pudimos construir cotas inferiores para el stock de capital humano agregado basadas únicamente en los años de estudio de la población de cada país, según las distintas posibles especificaciones de la ecuación de Mincer.

Las regresiones propuestas utilizando las cotas inferiores muestran coeficientes consistentes con la teoría económica. Con estos resultados, logramos construir las series correspondientes a las cotas superiores para cada especificación de la ecuación de Mincer considerada. Cuando consideramos en nuestra regresión las cotas superiores y las cotas inferiores obtenemos estimadores muy distintos. Sin embargo, la diferencia en el efecto de la educación sobre el PBI es mínima para cada especificación. Esto se debe a que los coeficientes estimados se reducen casi en la misma proporción en la que aumentamos los coeficientes de agregación.

Finalmente, incluimos una medida de calidad educativa basada en resultados de test de educación. Al incluir esta medida, los años de estudio dejan de ser un determinante significativo del PBI per cápita, salvo cuando consideramos la especificación cuadrática entre logaritmo del capital humano y los años de escolaridad de un individuo.

Los resultados obtenidos muestran que la mejor especificación posible, entre las estudiadas, para la ecuación de Mincer es la cuadrática. Bajo esta especificación, las regresiones realizadas muestran resultados consistentes con los hallados por Breton (2011), ya que con ella estimamos que tanto la calidad como la cantidad de educación parecen ser determinantes importantes del crecimiento económico. No obstante, es relevante mencionar que, debido a los problemas de endogeneidad presentes típicamente en regresiones que involucran series de tiempo agregadas, no es posible interpretar a los coeficientes hallados en las regresiones como efectos marginales o elasticidades. Por otro lado, también observamos que existen ciertas limitaciones en el cálculo de los posibles efectos que puede tener invertir en capital humano debido a la falta de datos desagregados relativos a calidad educativa.

La relación derivada en este trabajo entre años de estudio y capital humano demuestra que es necesario, al menos, contar con datos desagregados tanto de cantidad de años de educación como de su calidad para calcular el stock de capital humano agregado de una economía. Al tomar variables agregadas podemos estar incurriendo en nuevos sesgos que impactan en nuestras estimaciones y, además, hace imposible cualquier cálculo de corto plazo.

Por último, debemos mencionar que en este trabajo solo hemos considerado el impacto de la educación sobre el capital humano, sin considerar que existen otros factores que pueden afectarlo, como lo es la salud de los individuos. No obstante, incorporar salud en nuestro modelo requiere disponer de datos que vinculen la distribución del estado de salud de una población con la distribución de los años de estudio de aquella, así como estimaciones del impacto que tiene esta variable sobre la productividad individual.

Agradecimientos

Especialmente a los profesores Luis Alcalá, Virginia Vera, Marcos Herrera y Raimundo Soto, cuyos aportes y comentarios fueron esenciales para llevar a cabo este trabajo. Además, agradezco la ayuda recibida por parte de la Secretaría de Investigación, Internacionales y Posgrados de la Universidad Nacional de Cuyo.

Referencias

Alejo, J. y Funes, V. (2021). Ecuaciones Salariales de parejas bajo selección muestral bivariada. Una aplicación al caso argentino. Revista de Análisis Económico, 36(1), 3-22.

Altinok, N., Angrist, N. y Patrinos, H. (2018). Global data set on education quality (1965-2015) (Working Paper No. 8314). World Bank.

Angrist, N., Djankiv, S., Goldberg, P. y Patrinos, H. (2021). Measuring human capital using global learning data. Nature, 592, 403-408.

Barro, R. y Lee, J. (2013). A new data set of educational attainment in the world, 1950-2010. Journal of Development Economics, 104(C), 184-198.

Becker, G. (1962). Investment in Human Capital: A Theoretical Analysis. Journal of Political Economy, 70(5), 9-49.

Belzil, C. (2008). Testing the specification of the mincer wage equation. Annales d'Economie et de Statistique, (91/92), 427-451.

Benhabib, J. y Spiegel, M. (1994). The role of human capital in economic development: evidence from aggregate cross-country data. Journal of Monetary Economics, 34(2), 143-173.

Bils, M. y Klenow, P. (2000). Does schooling cause growth? American Economic Review, 90(5), 1160-1183.

Boot, J., Feibes, W. y Lisman, J. (1967). Further methods of derivation of quarterly figures from annual data. Applied Statistics, 16(1), 65-75.

Breton, T. (2011). The quality vs. the quantity of schooling: What drives economic growth? Economics of Education Review, 30(4), 765-773.

Choi, I. (2001). Unit root test for panel data. Journal of International Money and Finance, 20(2), 249-272.

Cohen, D. y Soto, M. (2007). Growth and human capital: good data, good results. Journal of Economic Growth, 12(1), 51-76.

Denton, F. (1971). Adjustment of monthly or quarterly series to annuals totals: An approach based on quadratic minimization. Journal of the American Statistical Association, 66(333), 99-102.

Deschenes, O. (2001). Unobserved ability, comparative advantage, and the rising return to education in the United States 1979-2000. Department of Economics, UC Santa Barbara.

Feenestra, R., Inklaar, R. y Timmer, M. (2015). The next generation of the Penn World Table. American Economic Review, 105(10), 3150-3182.

Hanushek, E. (2013). Economic growth in developing countries: The role of human capital. Economics of Education Review, 37(C), 204-212.

Hanushek, E. y Woessmann, L. (2008). The Role of Cognitive Skills in Economic Development. Journal of Economic Literature, 46(3), 607-668.

Jin, S., Phillips, P. y Sun, Y. (2006). A new approach to robust inference in cointegration. Economics Letters, 91(2), 300-306.

Kao, C. y Chiang, M. (2000). On the estimation and inference of cointegrated regression in panel data. En B. Baltagi (Ed.), Nonstationary Panels, Panel Cointegration, and Dynamic Panels (Advances in Econometrics) (pp. 161-178). JAI Press, Amsterdam.

Lindhal, M. y Krueger, A. (2001). Education for Growth: Why and for Whom? Journal of Economic Literature, 39(4), 1101-1136.

Lucas, R. (1988). On the mechanics of economic development. Journal of Monetary Economics, 22(1), 3-42.

Mincer, J. (1974). Schooling, experience, and earnings. National Bureau of Economic Research, Inc.

Montenegro, C. y Patrinos, H. (2014). Comparable estimate of returns to schooling around the world (Policy Research Working Paper Series No. 7020). World Bank.

Pedroni, P. (1999). Critical values for cointegration test in heterogeneous panels with multiple regressors. Oxford Bulletin of Economics and Statistics, 61(S1), 653-670.

Phillip, P. y Moon, H. (1999). Linear regression limit theory for nonstationary panel data (Cowless Foundation Discussion Papers No. 1222). Cowless Foundation for Research in Economics, Yale University.

Poschke, M. (2018). The firm size distribution across countries and skill-biased change in entrepreneurial technology. American Economic Journal: Macroeconomics, 10(3), 1-41.

Pritchett, L. (2001). Where all the education gone? The World Bank Economic Review, 15(3), 367-391.

Psacharopoulos, G. (1985). Returns to education: A further international update and implications. Journal of Human Resources, 20(4), 583-604.

Rodríguez Feijoo, S., Rodríguez Caro, A. y Dávila Quintana, C. (2001). Análisis comparativo de los métodos de desagregación temporal sin información auxiliar. Revista Electrónica de Comunicaciones y Trabajos de ASEPUMA, Actas, 9(1), 1-14.

Romer, P. (1990). Endogenous technological change. Journal of Political Economy, 98(5), 71-102.

Schultz, T. (1961). Investment in Human Capital. The American Economic Review, 51(1), 1-17.

Vera Rueda, M. J. (2015). En busca de lo inobservable: incorporando habilidades en un modelo à la Mincer. CAF Development Bank of Latin America.

World Bank (2020). The Human Capital Index 2020 Update: Human Capital in the Time of COVID-19. World Bank.

Apéndice

A. El método de Boot, Feibes y Lisman

En general, con el fin de obtener series de alta frecuencia en base a series originales de baja frecuencia Boot et al. (1967) proponen minimizar la suma de los cuadrados de las diferencias de los años sucesivos sujeto a la restricción de que la suma de los totales anuales obtenidos coincida con el total de los 5 años. No obstante, este método sirve para series de tipo flujo. Para el caso de series tipo stock, es conveniente primero diferenciar la serie y luego aplicar el método mencionado a la serie original. De esta forma se obtiene una estimación de la variación anual de la serie que coincide con la variación total cada 5 años. En términos matriciales, nuestro problema consiste en: ${\min }_x{x}^{\text{'}}{D}^{\text{'}}Dxs.a.Bx=Y$ donde $Y_{\left(10\times 1\right)}$ es el vector de variaciones cada 5 años de la serie original, $x_{\left(50\times 1\right)}$ es el vector de variaciones anuales a estimar,$D_{\left(50\times 50\right)}$ es la matriz que transforma al vector x en primeras diferencias y $B_{\left(10\times 50\right)}$ es la matriz que transforma las variaciones anuales en variaciones cada cinco años. La forma de las matrices $D$ y $B$ puede verse en Denton (1971). La solución a este problema viene dado por: $x={\left(D^{\text{'}}D\right)}^{-1}{B}^{\text{'}}{\left(B{\left(D^{\mathrm{\text{'}}}D\right)}^{-1}{B}^{\text{'}}\right)}^{-1}Y$

B. Test de raíz unitaria y cointegración

Cuadro A

Test de Choi de raíz unitaria

Elaboración propia en base a Barro y Lee (2013) y PWT 9.0.
Hipótesis nula: todos los paneles contienen raíz unitaria.

Cuadro B

Test de cointegración de Pedroni

Elaboración propia en base a Barro y Lee (2013) y PWT 9.0.
Test distribuidos $N\left(0,1\right)$ bajo la hipotesis nula de no cointegración.

C. simulaciones de Montecarlo

El objetivo de este apartado es demostrar mediante simulaciones de Montecarlo que se cumple la relación (29) para una estructura de datos similar a la analizada en este trabajo. Con este fin, propusimos el mismo proceso generador de datos que Kao y Chiang (2000) para paneles heterogéneos: $y_{it}=a_i+b{x}_{it}+{\mu }_{it},$ $x_{it}=x_{it-1}+{\nu }_{it}.$ donde $\left({\mu }_{it},{\nu }_{it}\right)$ sigue un proceso ARMA(1,1):

$\begin{array}{c}\left(\begin{array}{c}{\mu }_{it}\\ {\nu }_{it}\end{array}\right)=\left(\begin{array}{cc}0.5& 0\\ 0& 0.5\end{array}\right)\left(\begin{array}{c}{\mu }_{it-1}\\ {\nu }_{it-1}\end{array}\right)+\left(\begin{array}{c}{\mu }_{it}^{\mathrm{*}}\\ {\nu }_{it}^{\mathrm{*}}\end{array}\right)\left(\begin{array}{cc}0.3& -0.4\\ {\theta }_i& 0.6\end{array}\right)\left(\begin{array}{c}{\mu }_{it-1}^{\mathrm{*}}\\ {\nu }_{it-1}^{\mathrm{*}}\end{array}\right),\end{array}$

con:

$\begin{array}{c}\left(\begin{array}{c}{\mu }_{it}^{\mathrm{*}}\\ {\nu }_{it}^{\mathrm{*}}\end{array}\right)\sim N\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}1& {\sigma }_i\\ {\sigma }_i& 1\end{array}\right]\right).\end{array}$

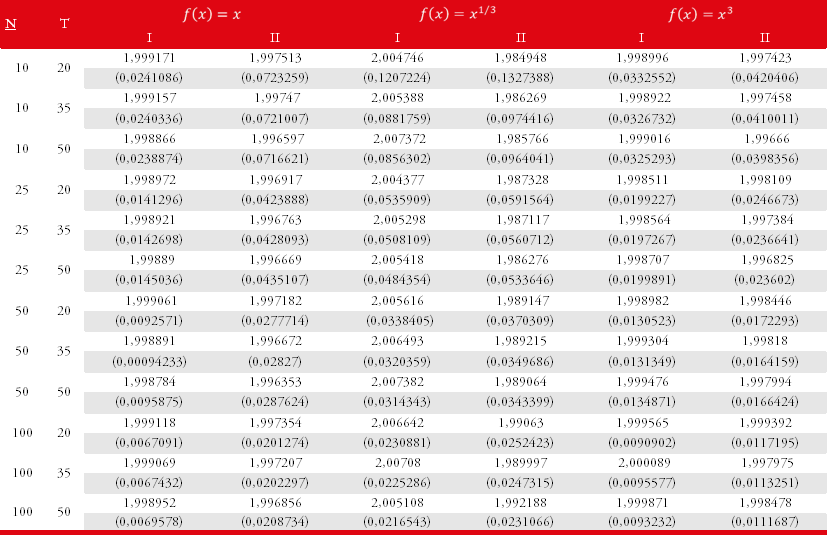
Siguiendo a (0,), fijamos $b=\; 2$, generamos $a_i$ de una distribución $U\left[0,10\right]$ y generamos a ${\theta }_i$ y ${\sigma }_i$, ambas de una distribución $U\left[-0.8,0.8\right]$. A continuación, construimos cotas, $x^{*}$, superiores e inferiores para $x$ mediante la siguiente especificación: $x_{maxit}^{\mathrm{*}}=x_{it}+c\times f\left(x_{it}\right),$ $x_{minit}^{\mathrm{*}}=x_{it}-d\times f\left(x_{it}\right).$ donde en cada replica generamos $c$ y $d$ a partir de distribuciones uniformes distintas para cada forma funcional de $f$, de forma tal que $\max \left(x_{\mathit{max}}^{*}/x_{it}\right)<\; 2$ y $\max \left(x_{\mathit{i}t}/x_{\mathit{min}}^{*}\right)<\; 2$. Debemos mencionar que propusimos 3 formas funcionales distintas para $f$: lineal, cúbica y raíz cubica. En cada réplica generamos $N\left(T+100\right)$ observaciones, que separamos en $N$ series, descartando las primeras 100 observaciones de cada serie. Por último, propusimos $N\in \left\{10,25,50,100\right\}$ y $T\in \left\{20,35,50\right\}$. De esta forma, los paneles de mayor tamaño son prácticamente iguales al estudiado en este trabajo. Finalmente, para cada simulación estimamos las siguientes regresiones por el método de MCOD(3,3): $y_{it}=a_i+b_M{x}_{maxit}^{\mathrm{*}}+{\mu }_{it}^{\mathrm{\text{'}}},$ $y_{it}=a_i+b_m{x}_{minit}^{\mathrm{*}}+{\mu }_{it}^{\mathrm{\text{'}}\mathrm{\text{'}}}$ Por la forma en que hemos construido las cotas y por el sesgo de variable omitida deducimos que:

$\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{m}{\widehat{b}}_M=b+\frac{\mathrm{C}\mathrm{o}\mathrm{v}\left(x_{max}^{\mathrm{*}},x_{max}^{\mathrm{*}}-x\right)}{\mathrm{V}\mathrm{a}\mathrm{r}\left(x_{max}^{\mathrm{*}}\right)}$(32)

$\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{m}{\widehat{b}}_m=b-\frac{\mathrm{C}\mathrm{o}\mathrm{v}\left(x_{min}^{\mathrm{*}},x-x_{min}^{\mathrm{*}}\right)}{\mathrm{V}\mathrm{a}\mathrm{r}\left(x_{min}^{\mathrm{*}}\right)}$(33)

Estas últimas dos ecuaciones implican que se cumple la relación (29). El siguiente cuadro muestra que para los paneles simulados se cumplen las ecuaciones (32) y (33) sin importar la forma funcional elegida para $f$. Debemos resaltar que realizamos 1000 réplicas por cada proceso propuesto.

Cuadro C

Simulaciones de Montecarlo

Nota: I: ${\widehat{b}}_M+b·\frac{\mathit{cov}\left(x_{max}^{\mathrm{*}},x_{max}^{\mathrm{*}}-x\right)}{\mathit{var}\left(x_{max}^{\mathrm{*}}\right)};$ II: ${\widehat{b}}_m-b·\frac{\mathit{cov}(x_{min}^{\mathrm{*}},x-x_{min}^{\mathrm{*}})}{\mathit{var}\left(x_{min}^{\mathrm{*}}\right)}$
Fuente: Elaboración propia.

Notas

1 Por construcción ${\psi }_j$ toma valores en el intervalo $[0,1]$ y el exponente en la expresión (21) es una función decreciente en este parámetro, por lo que sus valores extremos son $m_j$ cuando ${\psi }_j=\; 0$ y $\frac{m_j}{\alpha }$ cuando ${\psi }_j=\; 1$.

2 El máximo de años de estudio considerado por Barro y Lee (2013).

3 Notar que el supuesto de $n=\; 10$ es consistente con el modelo propuesto. En competencia perfecta, si cada empresa tiene n trabajadores habría entonces $N$ empresas en total, cada una demandando la misma cantidad de capital físico y humano, de forma tal que el producto agregado vendría dado por $Y=N{Y}_J=NA{K}_j^{1-\alpha }{H}_J^{\alpha }=A{\left(N{K}_j\right)}^{1-\alpha }{\left(N{H}_J\right)}^{\alpha }=A{K}^{1-\alpha }{H}^{\alpha }=Y$, donde $Y_J$, $K_J$ y $H_J$ corresponden al producto obtenido por la empresa $J$, y al capital físico y al capital humano demandado por dicha empresa respectivamente. Si bien n modifica al parámetro $\psi$, este solo genera cambios en cómo valoramos el stock de capital humano individual para llevar a cabo la agregación.

4 Utilizamos PBI per cápita y PBI por trabajador indistintamente, pero siempre haciendo referencia al último.

5 Se utilizaron 3 lags y 3 leads.

6 Trabajos como World Bank (2020) proponen una función de capital humano ampliada por calidad educativa que, en términos de nuestro trabajo, vendría dada por $h_{qj}=e^{g\left(s_j\right)\times q_j}$. No obstante, se optó por la forma funcional aquí propuesta porque ajusta mejor los datos en las estimaciones econométricas y permite diferenciar el efecto de aumentar los años de estudio de la población del de aumentar la calidad educativa de dichos años.

7 Los datos aquí utilizados fueron luego actualizados por Angrist et al. (2021). Sin embargo, estos autores presentan una base de datos que solo cubre el periodo 2000 - 2017.

Información adicional

Clasificación JEL: O2, I2, C2